Page 13 - 2025年第56卷第5期

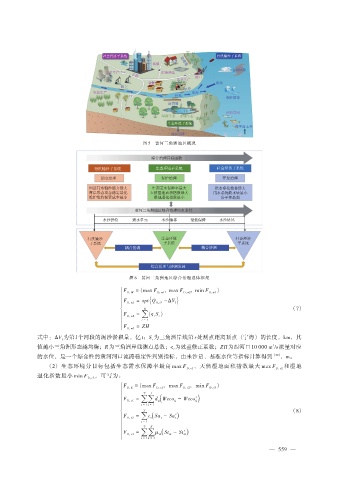
图 5 黄河三角洲地区概况

图 6 黄河三角洲地区综合治理总体框架

ìF = (max F ，max F ，min F )

ï ï D，W D，w1 D，w2 D，w3
ï ïF }
l
ï ï D，w1 = opt{Q ，-ΔV l
B，
í R （7）
ïF D，w2 ∑ (ς r S r )
ï
=
ï r = 1
ï
ï ï F D，w3 = ZH
î
式中：ΔV l 为第 l个河段的泥沙淤积量，亿 t；S r 为三角洲岸线第 r处测点距离顶点 （宁海） 的长度，km，其
值越小三角洲形态越均衡；R为三角洲岸线测点总数；ς r 为效益修正系数；ZH为西河口 10 000 m /s流量对应
3
的水位，是一个综合性的黄河河口流路稳定性判别指标，由来沙量、基准水位等指标计算得到 ［32］ ，m。
（2） 生态环境分目标包括生态需水保障率最高 max F 、天然湿地面积指数最大 max F 和湿地
D，e1 D，e2
退化指数最小 min F ，可写为：
D，e3
ìF = (max F ，max F ，min F )

ï D，E D，e1 D，e2 D，e3
ï
ï D，e1 ∑∑ d tj( )
T
J
ï
ï F = Weco tj - Weco′ tj
ï
ï t = 1 j = 1
ï
í T （8）
ï ï F D，e2 ∑ c t( Sa t - Sa′ t ) )
=
ï
ï
ï
t = 1
ï
K
T
ï
ï F
=
ï ï
D，e3 ∑∑ μ tk( St tk - St′ tk
î
t = 1 k = 1
— 559 —