Page 61 - 2025年第56卷第5期

综合实验数据与 ＡＵＣ － Ｓ曲线进行分析，实验数据的采样间隔为 ２ｓ，当 Ｗ＝ １５，Ｓ ＝ ５时，窗口覆
盖的时间与异常持续时间相匹配，理想状态下，在一个 “异常” 事件发生的 ３０ｓ内，算法会进行 ３次
检测并触发报警；而随 Ｓ增大，检测频率下降，当 Ｓ增大至 １５或更高时，窗口可能直接跃过异常发生
的时段，从而导致检测不到振动异常发生，导致 ＡＵＣ值降低。
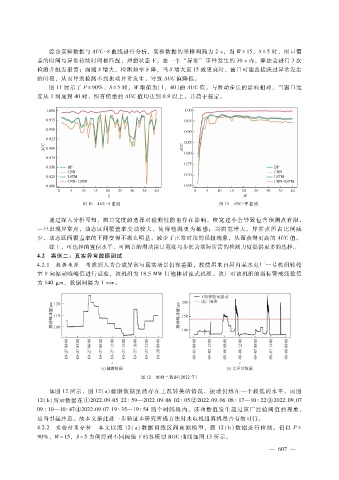
图 １１展示了 Ｐ ＝ ９０％、Ｓ ＝ ５ 时，Ｗ取值为［１，４０］的 ＡＵＣ值。与滑动步长的影响相对，当窗口宽
度从 １增加到 ４０时，所有模型的 ＡＵＣ值均达到 ０．９以上，并趋于稳定。

图 １０ ＡＵＣ － Ｓ曲线 图 １１ ＡＵＣ － Ｗ曲线

通过深入分析可知，窗口宽度的选择对检测性能也存在影响，窗宽过小会导致包含预测点有限，
一旦出现异常点，动态区间覆盖率变动较大，使得检测更为敏感；当窗宽增大，异常点所占比例减
少，动态区间覆盖率的下降变得不那么明显，减少了正常时段的误报现象，从而获得更高的 ＡＵＣ值。
综上，可选择的置信水平、可调节的滑动窗口宽度与步长为实际所需的检测力度提供更多的选择。
４．２ 案例二：真实异常数据测试
４．２．１ 数据来源 考虑到人为合成异常与真实场景仍有差距，故使用来自国内某水电厂一号机组转轮
室 Ｙ向振动峰峰值进行试验，该机组为 １８．５ＭＷ 灯泡体贯流式机组。该厂对该机组的指标警戒线数值
为 １４０μ ｍ，数据间隔为 １ｍｉｎ。

图 １２ 案例二数据（２０２２年）

如图 １２所示，图 １２（ａ）健康数据虽然存在工况转换的情况，振动仍然在一个较低的水平，而图
１２（ｂ）所示数据在 ①２０２２．０９．０５２２∶５９—２０２２．０９．０６０２∶０５ ② ２０２２．０９．０６０８∶１７—１０∶２２ ③ ２０２２．０９．０７
０９∶１０—１０∶４７ ④２０２２．０９．０７１９∶３５—１９∶５４四个时间段内，该项数值发生超过该厂经验阈值的现象，
应当引起注意。故本文借此进一步验证本研究所提方法对水电机组真机是否有效可行。
４．２．２ 实验结果分析 本文以图 １２（ａ）数据训练区间预测模型，图 １２（ｂ）数据进行检测。仍以 Ｐ＝
９０％，Ｗ＝ １５，Ｓ ＝ ５为例得到不同阈值下的各模型 ＲＯＣ曲线如图 １３所示。

— ６ ０ ７ —