Page 70 - 2025年第56卷第5期

接头试验基于修正惯用法，计算获取不同内水压方案下接头处轴力 N 与弯矩 M，轴力为 2 ~ 11 MN，
弯矩为 1.0 ~ 1.4 MN·m，且不考虑螺栓预紧力，本文选取文献［15］中 14 种典型方案进行验证分析，包
括 7 组正弯矩（SP1—SP7）与 7 组负弯矩试验（SN1—SN7），各方案受力状态见表 2 所示。可看出，方案
1 至方案 2 轴力小幅下降、弯矩显著提升，正弯矩工况由状态Ⅱ转变至状态Ⅲ；方案 2—7，轴力大幅
减小、弯矩基本保持不变，正、负弯矩工况逐渐转变至状态Ⅲ、Ⅳ，进入多层螺栓作用状态。

表 2 各验证方案所处状态
方案 轴力 N/MN 弯矩 M/（MN·m） 所处状态 方案 轴力 N/MN 弯矩 M/（MN·m） 所处状态
SP1 8.356 1.189 Ⅱ SN1 10.252 -1.083 Ⅱ

SP2 8.150 1.360 Ⅲ SN2 10.147 -1.248 Ⅱ
SP3 7.082 1.358 Ⅲ SN3 9.078 -1.246 Ⅱ
SP4 6.016 1.356 Ⅲ SN4 8.009 -1.243 Ⅱ
SP5 4.945 1.357 Ⅲ SN5 6.939 -1.245 Ⅲ
SP6 3.879 1.353 Ⅳ SN6 5.872 -1.242 Ⅲ
SP7 2.811 1.350 Ⅳ SN7 4.802 -1.238 Ⅲ

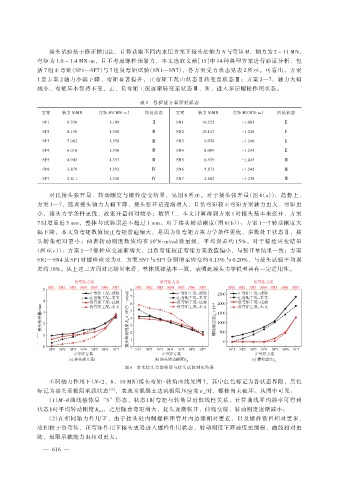
对比接头张开量、转动刚度与螺栓应变结果，见图 6 所示。对于接头张开量（图 6（a））：趋势上，
方案 1—7，随着接头轴力大幅下降，接头张开量逐渐增大，且负弯矩较正弯矩方案轴力更大、弯矩更
小，接头力学条件更优，故张开量相对较小；数值上，本文计算得到方案 1 时接头基本未张开，方案
7 时增至近 3 mm，整体与试验误差不超过 1 mm。对于接头转动刚度（图 6（b））：方案 1—7 转动刚度大
幅下降，本文负弯矩数值较正弯矩普遍偏大，是因为负弯矩方案力学条件更优，多数处于状态Ⅱ，接
头转角相对更小；两者转动刚度数值均在 10 N·m/rad 数量级，平均误差约 15%。对于螺栓应变结果
8
（图 6（c））：方案 1—7 螺栓应变逐渐增大，且负弯矩较正弯矩方案数值偏小，与张开量结果一致；方案
SN1—SN4 及 SP1 时螺栓应变为 0，方案 SN7 与 SP7 分别增至应变约 0.13% 与 0.20%，与接头试验平均误
差约 10%。从上述三方面对比结果来看，整体规律基本一致，表明此接头力学模型具有一定适用性。

图 6 本文接头力学模型与接头试验对比结果

不同轴力作用下（N=2、6、10 MN）接头弯矩-转角曲线见图 7，其中红色标记为各状态界限，黑色
标记为接头至极限承载状态 ［32］ ，表现为混凝土达到极限压应变 ε 时，螺栓尚未破坏。从图中可见：
cu
（1）M-θ 曲线整体呈“S”形态，状态 I 时弯矩与转角呈近似线性关系，计算曲线平均斜率可得到
状态 I 时平均转动刚度 K ，之后随着弯矩增大，接头逐渐张开，曲线变缓，转动刚度逐渐减小；
θ-I
（2）在相同轴力作用下，由于接头处内侧螺栓距管片内边缘相对更近，以及螺栓数目相对更多，
故相较于负弯矩，正弯矩作用下接头更易进入螺栓作用状态，转动刚度下降速度更缓慢，曲线相对更
陡，极限承载能力也相对更大；

— 616 —