Page 50 - 水利学报2021年第52卷第6期

4 数值模型

4.1 混凝土防渗墙塑性损伤模型 苗家坝防渗墙实测结果表明墙体一定区域内承受较大拉应力，可
能引起损伤或开裂。本文采用数值方法进一步揭示防渗墙的力学特性。数值计算中通常采用线弹性
模型模拟混凝土的应力变形关系，但是只有在小荷载作用下混凝土才展现线弹性行为，随着拉伸应
变的增加，混凝土将产生损伤和开裂 ［26］ 。因此，分析高土石坝混凝土防渗墙的力学性状时有必要考
虑材料的损伤行为。本文采用 Lee 等 ［29］ 提出的塑性损伤模型描述混凝土防渗墙的应力变形关系，该模
型可以考虑独立的压缩和拉伸损伤模式以及刚度恢复，已经应用于面板堆石坝面板的有限元损伤分
析中 ［30］ 。该模型中将应力应变关系表示为：
) (
)σ
σ = (1 - d ˉ = (1 - d E ε - ε p ) （1）
i
式中：σ为混凝土的应力；d 为一个表示弹性刚度减小的标量退化损伤变量； σ ˉ 为有效应力；E 为未
i
p
损伤的弹性刚度；为ε总应变；ε 为塑性应变。
模型引入损伤变量 k 描述混凝土的损伤状态，退化的损伤变量表示为：
n
ε p
k = g 1  σ dε p （2）
n
n
n 0
∞
n 
g = σ dε p （3）
n
0
)(
d = 1 - ( 1 - d ( ) 1 - sd ( ) ) （4）
k
k
C C T T
式中：n 为不同的状态，n 为 T 表示拉伸状态，n 为 C 表示压缩状态；g 为混凝土的耗散能量密度，可
n
以通过断裂能 G 与单个网格单元的特征长度 l 的比值确定；σ 为单轴应力；d 、d 分别为拉伸和压
n
n
n
C
T
缩单轴损伤变量；k 、k 分别为拉伸和压缩为损伤变量；s 为权重因子。
T C

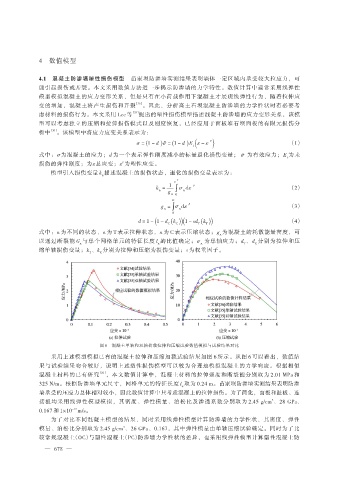
图 6 混凝土单轴和双轴荷载拉伸和压缩试验数值模拟与试验结果对比
采用上述模型模拟已有的混凝土拉伸和压缩加载试验结果如图 6 所示。从图 6 可以看出，数值结
果与试验结果吻合较好，说明上述塑性损伤模型可以较为合理地模拟混凝土的力学响应。根据相似
混凝土材料的已有研究 ［26］ ，本文数值计算中，混凝土材料的拉伸强度和断裂能分别取为 2.01 MPa 和
325 N/m。根据防渗墙单元尺寸，网格单元的特征长度 l 取为 0.24 m。苗家坝防渗墙实测结果表明防渗
n
墙承受的压应力总体相对较小，因此数值计算中只考虑混凝土的拉伸损伤。为了简化，面板和趾板、连
接板均采用线弹性模型模拟，其密度、弹性模量、泊松比及渗透系数分别取为 2.45 g/cm 、28 GPa、
3
-12
0.167 和 1×10 m/s。
为了对比不同混凝土模型的结果，同时采用线弹性模型计算防渗墙的力学性状，其密度、弹性
模量、泊松比分别取为 2.45 g/cm 、26 GPa、0.167，其中弹性模量由单轴压缩试验确定。同时为了比
3
较常规混凝土（OC）与塑性混凝土（PC）防渗墙力学性状的差异，也采用线弹性模型计算塑性混凝土防

— 678 —