Page 52 - 水利学报2021年第52卷第6期

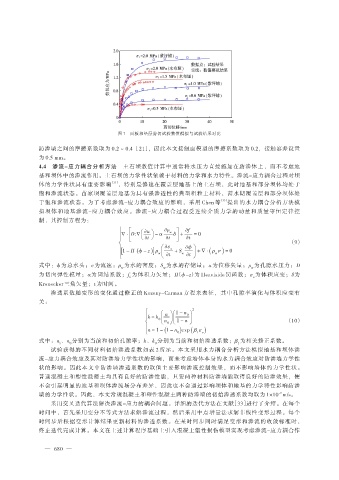
图 7 面板和垫层剪切试验数值模拟与试验结果对比

防渗墙之间的摩擦系数取为 0.2 ~ 0.4 ［21］，因此本文接触面模型的摩擦系数取为 0.2，接触容差设置
为 0.5 mm。
4.4 渗流-应力耦合分析方法 土石坝数值计算中通常将水压力直接施加在防渗体上，而不考虑地
基和坝体中的渗流作用。土石坝的力学性状依赖于材料的力学和水力特性。渗流-应力耦合过程对坝
体的力学性状具有重要影响 ［33］ ，特别是修建在覆盖层地基上的土石坝，此时地基和部分坝体均处于
饱和渗流状态。苗家坝覆盖层地基为具有强渗透性的典型粗粒土材料，蓄水期覆盖层和部分坝体处
于饱和渗流状态。为了考虑渗流-应力耦合效应的影响，采用 Chen 等 ［33］ 提出的水力耦合分析方法模
拟坝体和地基渗流-应力耦合效应。渗流-应力耦合过程受连续介质力学的动量和质量守恒定律控
制，其控制方程为：
ì é æ ∂u ö ∂p ù ∂f
ïÑ × ê D:Ñ - α w ú δ + = 0
ï ë è ∂t ø ∂t û ∂t
í （9）
ï æ ∂ε v ∂ϕ ö
)
ï[1 - H (ϕ - z ] ) ρ ç + S ÷ + Ñ × ( ρ ν = 0
î w è ∂t w ∂t ø w
式中：ϕ 为总水头；v 为流速；ρ 为水的密度；S 为水的存储量；u 为位移矢量；p 为孔隙水压力；D
w w w
为切向弹性模量；α为固结系数；f 为体积力矢量；H（ϕ -z）为 Heaviside 罚函数；ε 为体积应变；δ为
b
v
Kronecker 三角矢量；t 为时间。
渗透系数随变形的变化通过修正的 Kozeny-Carman 方程来表征，其中孔隙率演化与体积应变有
关：
ì æ n öæ 1 - n ö 2
ïk ÷ç 0 ÷
ï = k ç
í 0 è n 0 øè 1 - n ø （10）
ï )
ï
î n = 1 - (1 - n 0 )exp( β ε v
1
式中：n 、n 分别为当前和初始孔隙率；k、k 分别为当前和初始渗透系数；β 为相关修正系数。
i
1
0
0
试验获得的不同材料初始渗透系数如表 2 所示。本文采用水力耦合分析方法模拟地基和坝体渗
流-应力耦合效应及其对防渗墙力学性状的影响，而未考虑墙体本身的水力耦合效应对防渗墙力学性
状的影响。因此本文中防渗墙渗透系数的取值主要影响渗流控制效果，而不影响墙体的力学性状。
普通混凝土和塑性混凝土均具有良好的防渗性能，只要两种材料防渗墙能取得良好的防渗效果，便
不会引起明显的地基和坝体渗流场分布差异，因此也不会通过影响坝体和地基的力学特性影响防渗
墙的力学性状。因此，本文常规混凝土和塑性混凝土两种防渗墙的初始渗透系数均取为 1×10 m/s。
-9
采用交叉迭代算法解决渗流-应力的耦合问题。详细的迭代方法在文献［33］进行了介绍。在每个
时间中，首先采用变分不等式方法求解渗流过程，然后采用中点增量法求解非线性变形过程。每个
时间步后根据变形计算结果更新材料的渗透系数。在某时间步同时满足变形和渗流的收敛标准时，
终止迭代完成计算。本文在上述计算程序基础上引入混凝土塑性损伤模型实现考虑渗流-应力耦合作

— 680 —