Page 78 - 2022年第53卷第5期

（１）地貌单元丰富度指数（Ｒ）。地貌单元丰富度指数（Ｒ）指在给定范围内观察到的地貌单元类型数
与整体最大类型数相比的情况，表达式如下：
Ｒ ＝ Σ ＮＴ ?ｎ （３）
ＧＵ
式中：ＮＴ 为所研究区域内地貌单元类型总数（例如，在存在浅滩，深潭和急滩的情况下，ＮＴ ＝ ３ ）；
ＧＵ
ＧＵ
ｎ为地貌单元类型的最大数量。
（ ２）地貌单元密度指数（Ｄ）。地貌单元密度指数（Ｄ）是指计算每单位长度调查范围内的地貌单元
总数（与类型无关），表达式如下：
Ｄ ＝ Σ Ｎ ?Ｌ （４）
ＧＵ
式中：Ｎ 为沿调查的范围观察到的地貌单元总数（如，对于 ５个浅滩、５个深潭和 ５个边滩，Ｎ ＝ １５ ）；
ＧＵ ＧＵ
Ｌ为所调查的范围（或子范围），ｋｍ。
（ ３）地貌单元多样性指数（Ｈ ）。Ｓｈａｎｎｏｎ多样性指数可用来反映景观异质性的程度，其值越大，
ｄ
景观异质性程度越好，景观内的生物越能稳定生存，景观异质性包含空间异质性。地貌单元多样性指
数（ Ｈ ）是基于 Ｓｈａｎｎｏｎ多样性指数提出的，表达式如下：
ｄ
ｍ
Ｈ ＝－ ＰｌｏｇＰ （５）
ｄ ∑ ＝１ ｉ ２ ｉ
ｉ
Ｐ＝ Ａ?ＴＡ ｊ （６）
ｉ
ｉ
式中：ｍ为研究区域地貌单元类型的总数；Ｐ为地貌单元类型 ｉ的面积（Ａ）所占研究河段总面积（ＴＡ）
ｉ ｉ ｊ
的比例。
３ 结果分析

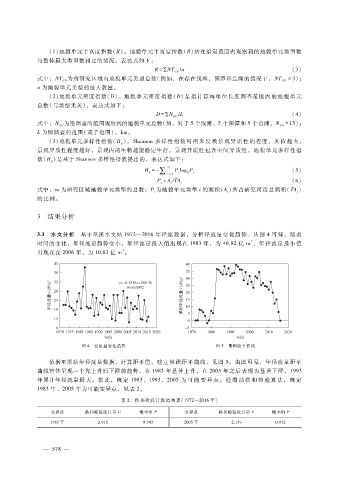
３．１ 水文分析 基于巫溪水文站 １９７２—２０１６年径流数据，分析径流量变化趋势。从图 ４可知，随着
３
时间的变化，年径流量趋势变小，年径流量最大值出现在 １９８３年，为 ４０．８２亿 ｍ ，年径流量最小值
３
出现在在 ２００６年，为 １０．８３亿 ｍ 。

图 ４ 径流量变化趋势 图 ５ 累积距平曲线

依据巫溪站年径流量数据，计算距平值，建立累积距平曲线，见图 ５。由图可见，年径流量距平
曲线整体呈现一个先上升后下降的趋势，在 １９８３年显著上升，在 ２００５年之后表现为显著下降，１９９３
年累计年径流量最 大。据 此，确 定 １９８３、１９９３、２００５为 可 能 变 异 点。经 滑 动 秩 和 检 验 算 法，确 定
１９８３年、２００５年为可能变异点，见表 ２。
表 ２ 秩和检验计算结果表（１９７２—２０１６年）

变异点 秩和检验统计量 Ｕ 概率值 Ｐ 变异点 秩和检验统计量 Ｕ 概率值 Ｐ
１９８３年 ２．０１８ ０．０４３ ２００５年 ２．１３９ ０．０３２

— ５ ７ —
８