Page 86 - 2022年第53卷第9期

图 １５ 数值结果与试验结果对比验证 图 １６ 不同装药结构下的损伤云图

为验证所选参数的可靠性，参考 Ｂａｎａｄａｋｉ等 ［２２］ 室内试验建立相关数值模型，并采用上述材料参
数进行调整试算。计算结果如图 １５所示，从图中可以看出，数值模拟与现场试验中，炮孔周围形成
了明显的粉碎区和破裂区由于室内试验中岩体试样本身存在缺陷，故产生了较多微裂隙，但整体上数
值模拟与现场试验主裂纹的扩展规律基本一致。此外，通过数值模拟计算所得粉碎区半径约为 ４．５倍
的炮孔半径，而 Ｂａｎａｄａｋｉ等 ［２２］ 试验中的粉碎区半径为 ５～６倍炮孔半径，综上可知，本文的计算模型
及相关参数选取是合理的。

４ 不同边界条件下的爆破动力响应分析

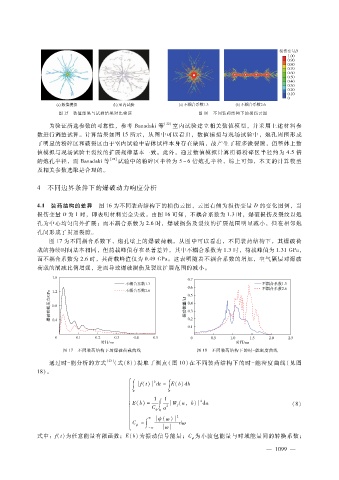
４．１ 装药结构的差异 图 １６为不同装药结构下的损伤云图，云图右侧为损伤变量 Ｄ的变化图例，当
损伤变量 Ｄ为 １时，即表明材料完全失效。由图 １６可知，不耦合系数为 １．３时，爆破损伤及裂纹以炮
孔为中心均匀向外扩展；而不耦合系数为 ２．６时，爆破损伤及裂纹的扩展范围明显减小，但在相邻炮
孔间形成了贯通裂隙。
图 １７为不同耦合系数下，炮孔壁上的爆破荷载。从图中可以看出，不同装药结构下，其爆破荷
载的持续时间基本相同，但荷载峰值存在显著差异，其中不耦合系数为 １．３时，荷载峰值为 １．３１ＧＰａ，
而不耦合系数为 ２．６时，其荷载峰值仅为 ０．４９ＧＰａ。这表明随着不耦合系数的增加，空气隔层对爆破
荷载的削减比例增强，进而导致爆破损伤及裂纹扩展范围的减小。

图 １７ 不同装药结构下的爆破荷载曲线 图 １８ 不同装药结构下的时－ 能密度曲线

通过时－ 能分析的方式 ［２３］ （式（８））提取了测点（图 １０）在不同装药结构下的时 － 能密度曲线（见图
１８）。
∫ ２ ∫
ｆ（ｔ） ｄｔ ＝ Ｅ（ｂ）ｄｂ
Ｒ Ｒ
１ １
２
Ｅ （ｂ） ＝ ∫ Ｗ（ａ，ｂ） ｄａ （８）
ｆ
２
Ｃ ａ
ψ Ｒ
∞ ψ （ ω ） ２
ψ ∫
Ｃ ＝ ｄ ω
－ ∞ ω
式中：ｆ（ｔ）为任意能量有限函数；Ｅ（ｂ）为振动信号能量；Ｃ 为小波包能量与时域能量间的转换系数；
ψ
０
— １ ９ ９ —