Page 73 - 2022年第53卷第11期

研究建立了一维非线性压密释水模型模拟压密释水过程 ［２２，２６］ 。
含水层系统的压密释水过程是含水层骨架所受有效应力变化的过程。当深层地下水开采发生后，
承压水位开始下降，孔隙水压力减小，即孔隙水所能分担的应力减小，这部分应力将转移到土体骨
架，使有效应力增加，从而压缩多孔介质，引起含水层压密释水，地面发生沉降。含水层系统的地质
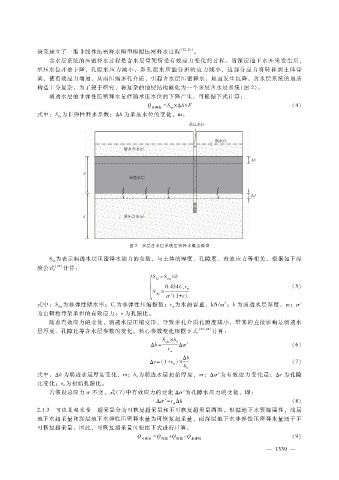
构造十分复杂，为了便于研究，将复杂的地层结构概化为一个多层含水层系统（图 ２）。
弱透水层的非弹性压密释水量伴随承压水位的下降产生，可根据下式计算：
Ｑ 非弹性 ＝ Ｓ × Δ ｈ × Ｆ （４）
ｋｖ
式中：Ｓ 为非弹性释水系数；Δ ｈ为承压水位的变化，ｍ。
ｋｖ

图 ２ 多层含水层系统压密释水概念模型
Ｓ 为表示弱透水层压密释水能力的参数，与土体的厚度、孔隙度、有效应力等相关，根据如下经
ｋｖ
验公式 ［２７］ 计算：
Ｓ ＝ Ｓ × ｂ
Ｓ ＝ { ０．４３４Ｃｒ （５）
ｋｖ
ｓｋｖ
ｃ ｗ
ｓｋｖ
σ ′（１ ＋ ｅ）
３
式中：Ｓ 为非弹性储水率；Ｃ为非弹性压缩指数；ｒ为水的容重，ｋＮ?ｍ ；ｂ为弱透水层厚度，ｍ；σ ′
ｓｋｖ
ｗ
ｃ
为由颗粒骨架承担的有效应力；ｅ为孔隙比。
随着有效应力的变化，弱透水层压缩变形，导致多孔介质孔隙度减小，带来的直接影响是弱透水
层厚度、孔隙比等含水层参数的变化。核心参数变化根据下式 ［２７ － ２８］ 计算：
Ｓ × ｂ ０
ｓｋｖ
Δ ｂ ＝ Δσ ′ （６）
ｒ
ｗ
Δ ｂ
Δ ｅ ＝ （１ ＋ ｅ） × （７）
０
ｂ
０
式中：Δ ｂ为弱透水层厚度变化，ｍ；ｂ为弱透水层初始厚度，ｍ；Δσ ′为有效应力变化量；Δ ｅ为孔隙
０
比变化；ｅ为初始孔隙比。
０
若假设总应力 σ不变，式（７）中有效应力的变化 Δσ ′为孔隙水压力的变化，即：
Δσ ′ ＝ ｒΔ ｈ （８）
ｗ
２．１．３ 可恢复超采量 超采量分为可恢复超采量和不可恢复超采量两类，根据地下水资源属性，浅层
地下水超采量和深层地下水弹性压密释水量为可恢复超采量，而深层地下水非弹性压密释水量属于不
可恢复超采量。因此，可恢复超采量可根据下式进行计算：
Ｑ ＝ Ｑ ＋ Ｑ － Ｑ （９）
可恢复 浅超 深超 非弹性
３
— １ ３ ９ —