Page 93 - 2023年第54卷第4期

＃
由图 ８可知，３监测点位移最大，累积位移曲线呈现明显的 “台阶状” 特征，且跃迁阶段与降雨
＃
＃
量较大时间段呈一一对应关系；１监测点的位移最小，累积位移曲线的阶跃型特征不明显；２监测点
的位移大小处于两者之间，累积位移曲线呈现轻微的跃迁状。由此可见，相对稳定监测点的变形受降
雨量影响较小，相对不稳定监测点受周期性降雨的影响较大；另外，单个监测点并不能反映坡体整体
的变形特征，有必要将多个监测点数据进行融合分析，以体现一定范围内的坡体整体变形演化趋势。
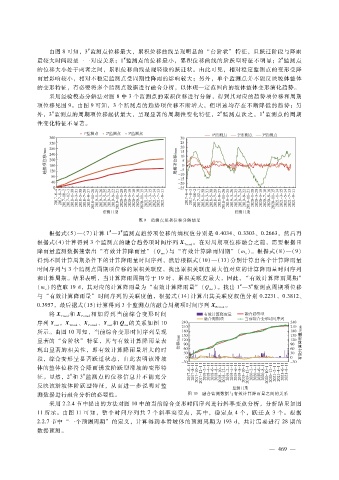
采用经验模态分解法对图 ８中 ３个监测点的累积位移进行分解，得到其对应的趋势项位移和周期
项位移见图 ９。由图 ９可知，３个监测点的趋势项位移不断增大，但增速均存在不断降低的趋势；另
＃
＃
＃
外，３监测点的周期项位移起伏最大，呈现显著的周期性变化特征，２监测点次之，１监测点的周期
性变化特征不显著。

图 ９ 监测点累积位移分解结果
＃
＃
根据式（５）—（７）计算 １—３监测点趋势项位移的熵权值分别是 ０．４０３４、０．３３０３、０．２６６３，然后再
根据式（４）计算得到 ３个监测点的融合趋势项时间序列 Ｘ Ｔｒｅｎｄ 。在对周期项位移融合之前，需要根据日
降雨量监测数据搜索出 “有效计算降雨量” （Ｑ ）与 “有效计算降雨周期” （ｍ ）。根据式（８）—（９）
ｍｅ ｅ
得到不同计算周期条件下的计算降雨量时间序列，然后根据式（１０）—（１３）分别计算出各个计算降雨量
时间序列与 ３个监测点周期项位移的累积关联度，找出累积关联度最大值对应的计算降雨量时间序列
和计算周期。结果表明，当计算降雨周期等于 １９时，累积关联度最大，因此， “有效计算降雨周期”
＃
＃
（ｍ）的值取 １９ｄ，其对应的计算降雨量为 “有效计算降雨量” （Ｑ ）。找出 １—３监测点周期项位移
ｅ ｍｅ
与 “有效计算降雨量” 时间序列的关联度值，根据式（ １４）计算出其关联度权值分别 ０．２２３１、０．３８１２、
０．３９５７，最后据式（１５）计算得到 ３个监测点的融合周期项时间序列 Ｘ Ｐｅｒｉｏｄ 。
将 Ｘ Ｔｒｅｎｄ 和 Ｘ Ｐｅｒｉｏｄ 相 加得 到当前 综合变 形时间
序列 Ｙ 。Ｘ 、Ｘ 、Ｙ 和 Ｑ 的关系如图 １０
ｃｕｒ Ｔｒｅｎｄ Ｐｅｒｉｏｄ ｃｕｒ ｍｅ
所示。由图 １０可知，当前综合变形时间序列呈现
显著的 “台阶状” 特征，其与有效计算降雨量表
现出显著的相关性，即有效计算降雨量增大的时
段，综合变形呈显著跃迁状态，由此表明该滑坡
体的整体位移符合降雨诱发阶跃型滑坡的变形特
＃
＃
征。显然，２和 ３监测点的位移信息并不能充分
反映该滑坡体阶跃型特征，从而进一步说明对监
测数据进行融合分析的必要性。 图 １０ 融合监测数据与有效计算降雨量之间的关系
采用 ２．２．４节中提出的方法对图 １０中的当前综合变形时间序列进行斜率变点分析，分析结果如图
１１所示。由图 １１可知，整个时间序列共 ７个斜率突变点，其中，稳定点 ４个，跃迁点 ３个。根据
２．２．７节中 “一个预测周期” 的定义，计算得到本滑坡体的预测周期为 １９３ｄ，共计需要进行 ２８期的
数据预测。

— ４ ６ ９ —