Page 93 - 2023年第54卷第7期

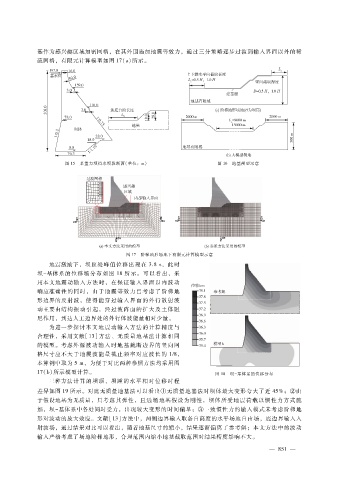
基作为感兴趣区域加密网格，在其外围施加地震等效力，通过三分策略逐步过渡到输入界面以外的稀
疏网格，有限元计算模型如图 １７（ａ）所示。

图 １５ 某重力坝挡水坝段断面（单位：ｍ） 图 １６ 地基模型示意

图 １７ 阶梯地形场地下有限元计算模型示意

地震激励下，坝顶处峰值位移出现在 ３．８ｓ，此时
坝－ 基体系的位移场分布如图 １８所示。可以看出，采
用本文地震动输入方法时，在保证输入界面以内波动
响应准确性的同时，由于地震等效力已考虑了阶梯地
形边界的反射波，使得能穿过输入界面的外行散射波
动主要由结构振动引起，经过波阵面的扩大及土体阻
尼作用，到达人工边界处的外行体波能量相对少量。
为进一步探讨本文地震动输入方法的计算精度与
合理性，采用文献［ １３］方法、无质量地基法计算相同
的模型。考虑外源波动输入时地基截断边界的竖向网
格尺寸应不大于地震波能量截止频率对应波长的 １?８，
本算例中取为 ５ｍ，为便于对比两种参照方法均采用图
１７（ｂ）所示模型计算。
图 １８ 坝－ 基体系的位移分布
三种方法计算的坝顶、坝踵的水平相对位移时 程
差异如图 １９所示。对比无质量地基法可以看出①无质量地基法对坝体最大变形夸大了近 ４５％；②由
于假设地基为无质量，只考虑其弹性，且远场地基假设为刚性，坝体所受地震荷载以惯性力方式施
加，坝－ 基体系中各处同时受力，出现较大变形的时间偏早；③一致惯性力的输入模式未考虑阶梯地
形对波动的放大效应。文献［ １３］方法中，两侧边界输入取各自高度的水平场地自由场，底边界输入入
射波场，通过结果对比可以看出，随着地基尺寸的缩小，结果逐渐偏离了参考解；本文方法中的波动
输入严格考虑了场地阶梯地形，合理范围内缩小地基截取范围对结果精度影响不大。

— ８ ５ １ —