Page 91 - 2023年第54卷第7期

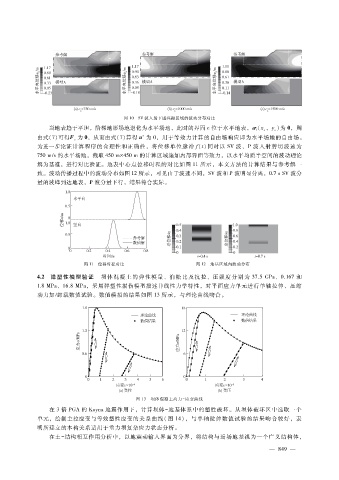
图 １０ ＳＶ波入射下感兴趣区域的波动分布对比
（ｘ，ｙ）为 ０，则
当地表趋于平坦，阶梯地形场地退化为水平场地，此时的界面 ｃ位于水平地表，σ ｆ
ｃ ｃ
ｓ
由式（７）可得Ｆ 为 ０，从而由式（７）算得 ｕ 为 ０，用于等效力计算的自由场响应即为水平场地的自由场。
ｃ
为进一步论证计算程序的合理性和正确性，将位移单位脉冲 ｆ（ｔ）同时以 ＳＶ波、Ｐ波入射剪切波速为
７５０ｍ?ｓ的水平场地，截取 ４５０ｍ × ４５０ｍ的计算区域施加内部界面等效力，以水平均质半空间的波动理论
解为基准，进行对比验证。地表中心点位移时程的对比如图 １１所示，本文方法的计算结果与参考解一
致。波动传播过程中的波动分布如图 １２所示，可见由于波速不同，ＳＶ波和 Ｐ波明显分离，０．７ｓＳＶ波分
量的波峰到达地表，Ｐ波分量下行，结果符合实际。

图 １１ 位移时程对比 图 １２ 地基区域内波动分布
４．２ 弹塑性模型验证 坝体混凝土的弹性模量、泊松比及抗拉、压强度分别为 ３７．５ＧＰａ、０．１６７和
１．８ＭＰａ、１６．８ＭＰａ，采用弹塑性损伤模型描述非线性力学特性，对平面应力单元进行单轴拉伸、压缩
动力加?卸载数值试验。数值模拟的结果如图 １３所示，与理论曲线吻合。

图 １３ 坝体混凝土应力－ 应变曲线
在 ３倍 ＰＧＡ的 Ｋｏｙｎａ地震作用下，计算坝体－ 地基体系中的塑性破坏。从坝体破坏区中选取一个
单元，绘制主拉应变与等效塑性应变的关系曲线（图 １４），与单轴拉伸数值试验的结果吻合较好，表
明所建立的本构关系适用于重力坝复杂应力状态分析。
在土－ 结构相互作用分析中，以地震动输入界面为分界，将结构与近场地基视为一个广义结构体，

— ８ ４ ９ —