Page 128 - 2023年第54卷第10期

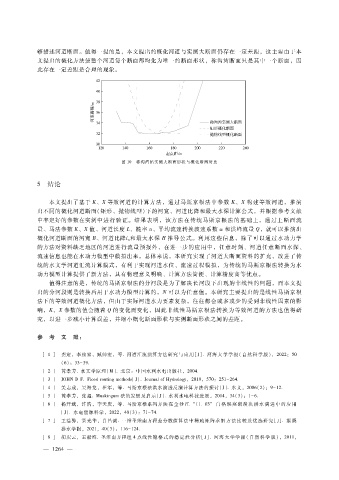
够描述河道断面。值得一提的是，本文提出的概化河道与实测大断面仍存在一定差距，这主要由于本
文提出的概化方法使整个河道每个断面都均化为唯一的断面形状，称沟湾断面只是其中一个断面，因
此存在一定差距是合理的现象。

图 １０ 称沟湾站实测大断面形状与概化断面对比

５ 结论

本文提出了基于 Ｋ、Ｘ等效河道的计算方法，通过马斯京根法中参数 Ｋ、Ｘ构建等效河道，推演
出不同的概化河道断面（矩形、抛物线型）下的河宽、河道比降和最大水深计算公式，并根据参考文献
中率定好的参数在实例中进行验证。结果表明，该方法在传统马斯京根法的基础上，通过上断面流
量、马法参数 Ｋ、Ｘ值、河道长度 Ｌ、糙率 ｎ、平均流速转换波速系数 α和洪峰流量 Ｑ，就可以推演出
概化河道断面的河宽 Ｂ、河道比降ｉ和最大水深 Ｈ推导公式。利用这些信息，除了可以通过水动力学
０
的方法对资料缺乏地区的河道进行流量预报外，在进一步的应用中，任意时刻、河道任意断面水深、
流速信息也能在水动力模型中模拟出来。总体来说，本研究实现了河道大断面资料的扩充，改进了传
统的水文学河道汇流计算模式，有利于实现河道水位、流速过程模拟，为传统的马斯京根法转换为水
动力模型计算提供了新方法，具有物理意义明确、计算方法简便、计算精度高等优点。
值得注意的是，传统的马斯京根法的分河段是为了解决长河段下出现的非线性的问题，而本文提
出的分河段则是转换后用于水动力模型计算的，Ｎ可以为任意值。本研究主要提出的是线性马斯京根
法下的等效河道概化方法，但由于实际河道水力要素复杂，往往都会或多或少的受到非线性因素的影
响，Ｋ、Ｘ参数的值会随着 Ｑ的变化而变化，因此非线性马斯京根法转换为等效河道的方法也值得研
究，以进一步减小计算误差，并缩小概化断面形状与实测断面形状之间的差距。

参 考 文 献：

［ １］ 龚定，李致家，臧帅宏，等．河道汇流演算方法研究与应用［Ｊ］．河海大学学报（自然科学版），２０２２：５０
（６）：３３ － ３９．
［ ２］ 芮孝芳．水文学原理［Ｍ］．北京：中国水利水电出版社，２００４．
［ ３］ ＪＯＨＮＤＦ．Ｆｌｏｏｄｒｏｕｔｉｎｇｍｅｔｈｏｄｓ［Ｊ］．ＪｏｕｒｎａｌｏｆＨｙｄｒｏｌｏｇｙ，２０１９，５７０：２５１ － ２６４．
［ ４］ 关志成，吴海龙，崔军，等．马斯京根法洪水演进反演计算方法的探讨［Ｊ］．水文，２００６（２）：９ － １２．
［ ５］ 芮孝芳，张超．Ｍｕｓｋｉｎｇｕｍ法的发展及启示［Ｊ］．水利水电科技进展，２０１４，３４（３）：１ － ６．
［ ６］ 杨开斌，许浩，李天庆，等．马斯京根系列方 法 在 金 沙 江 “１１．０３” 白 格 堰 塞 湖 溃 决 洪 水 演 进 中 的 应 用
［ Ｊ］．水电能源科学，２０２２，４０（３）：７１ － ７４．
［ ７］ 王浩骅，管光华，肖昌诚．一维圣维南方程差分数值算法中稀疏矩阵求解方法比较及优选研究［Ｊ］．灌溉
排水学报，２０２１，４０（３）：１１６ － １２４．
［ ８］ 胡庆云，王船海．圣维南方程组 ４点线性隐格式的稳定性分析 ［Ｊ］．河海大学学报 （自然科学版），２０１１，

— １ ２ ４ —
６