Page 126 - 2023年第54卷第10期

结果较好，与文献［２２］方法演算结果相差不大，能反应临清出流过程。
表 １ 秤钩湾—临清流量计算结果对比

指标 文献 ［２２］ 演算临清流量 本文方法演算临清流量（矩形） 本文方法演算临清流量（抛物线型）
ＲＭＳＥ ６．０７ １０．７１ １０．７６

Ｒ ２ ０．９９ ０．９９ ０．９９
ｎ
∑ （Ｑ（ｉ） － Ｑ １ （ｉ）） ２
ｉ ＝１
２
２
注：可决系数 Ｒ ＝１ － ∑ ［Ｑ（ｉ） － Ｑ １ （ｉ）］? ∑ ［Ｑ（ｉ） － ＡＱ ］，式中 ＡＱ是出流的平均流量；均方根误差 ＲＭＳＥ＝ 槡 ｎ
２
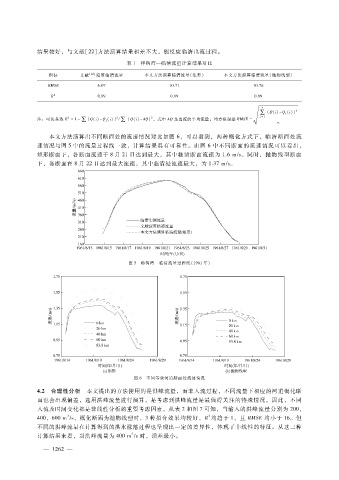
本文方法演算出不同断面处的流速情况对比如图 ６，可以看到，两种概化方式下，临清断面处流
速情况与图 ５中的流量过程线一致，计算结果具有可靠性。由图 ６中不同断面的流速情况可以看出，
矩形断面下，各断面流速于 ８月 ２１日达到最大，其中临清断面流速为 １．６ｍ?ｓ。同时，抛物线型断面
下，各断面在 ８月 ２２日达到最大流速，其中临清处流速最大，为 １．３７ｍ?ｓ。

图 ５ 称沟湾—临清流量过程线（１９６１年）

图 ６ 不同等效河道断面处流速情况

４．２ 合理性分析 本文提出的方法使用的是洪峰流量，而非入流过程，不同流量下相应的河道概化断
面也会出现偏差，选用洪峰流量进行演算，是考虑到洪峰流量是最值得关注的特殊情况。因此，不同
入流及时间变化都是非线性分析的重要考虑因素。从表 ２和图 ７可知，当输入的洪峰流量分别为 ２００，
３
２
４００，６００ｍ ?ｓ，概化断面为抛物线型时，３种拟合效果均较好，Ｒ均趋于 １，且 ＲＭＳＥ均小于 １６。但
不同的洪峰流量在计算得到的洪水涨落过程也呈现出一定的差异性，体现了非线性的特征。从这三种
３
计算结果来看，当洪峰流量为 ４００ｍ ?ｓ时，误差最小。
６
— １ ２ ２ —