Page 114 - 2023年第54卷第12期
P. 114
武 [29] 早期从理论上推导出通过水流因子计算冲积河流 D 的公式,得到较多资料的验证。显然可利用
50
这一造床流量下 D 与水力因子的量化关系,反求相应的河床比降 i,亦即:
50 0
4.9D m
i = (10)
0
h
0
黄河水文站观测断面基本上都布置在一岸或两岸建有丁坝的河段上,其局部水头损失往往对水力
能坡 I产生一定影响,故计算 I时除体现河床比降的主导影响外,还应考虑边岸局部水头损失的作用。
按照黄河动床模型试验结果 [15] 和局部水头损失的表达形式,将其修正式近似表示为:
V 2
I = i + (11)
0
2g Δ l
式中 Δ l为流速水头对应的相对长度,应跟河槽宽度 B有关,参照河工模型对进口段长度 “宜在模型
c
河段宽度 3~5倍” [45] 的要求,取 Δ l = 4B,黄河下游宽河段,B一般为 2500m [46] ,可取 Δ l = 10km;
c
c
黄河下游两岸建有坝垛的窄河段,B一般为 500m,取 Δ l = 2000m ;艾山水文断面河宽 400m,左岸建
c
有坝垛,下游约 500m处有外山和井圈险工相对,形成著名的艾山卡口,高水位时壅水严重,所以艾
山水文断面取 Δ l = 10km。黄河上、中游,渭河和长
江为便于计算,暂均取 Δ l = 10km。
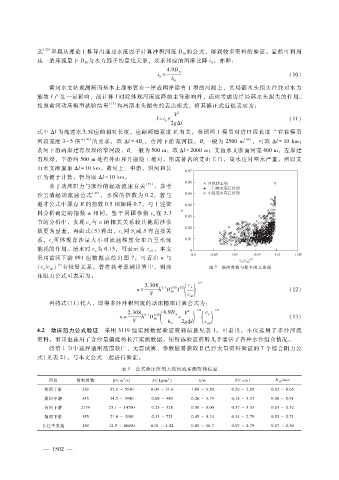
鉴于动床阻力与床沙的起动流速有关 [39] ,参考
沙玉清起动流速公式 [47] ,水深的指数为 0.2,若与
谢才公式中原有 R的指数 0.5相加得 0.7,与上述资
料分析确定的指数 α相同。鉴于涡团参数 c在 3.3
n
节的分析中,发现 c与 n的相关关系较其他泥沙参
n
数更为显著,再由式( 5)看出,c同 S或 S有直接关
n
v
系,c可体现含沙量大小对流速梯度分布乃至水流
n
能耗的作用。清水时 c为 0.15,可表示为 c ,本文
n n0
采用黄河下游 991组数据点绘出图 7。可看出 n与
1?3
( c?c ) 有较好关系。若将其考虑到计算中,则动 图 7 涡团参数与糙率的关系图
n0
n
床阻力公式可表示为:
2 .308 c 1?3
n
1?10 1?2
0.7
n = h D I ( ) (12)
50
V c
n0
再将式(11)代入,即得多沙冲积河流的动床糙率计算公式为:
2 .308 4.9D m V 2 1?2 c 1?3
n
0.7
n = h D 1?10 ( + ) ( ) (13)
50
V h 2g Δ l c
0 n0
4.2 动床阻力公式验证 采用 3119组实测数据验证资料信息见表 1。可看出,不仅选用了多沙河流
资料,而且也选用了含沙量偏低的长江实测数据,使所选验证资料几乎囊括了各种水沙组合情况。
将第 1节中选择适用范围较广、无需试算、参数较易获取且已经大量资料验证的 7个综合阻力公
式(见表 2),与本文公式一起进行验证。
表 1 公式验证所用天然河流实测资料信息
3
3
河段 资料组数 Q?(m ?s) S?(kg?m ) h?m V?(m?s) D 50 ?mm
黄河上游 330 52.1~5130 0.04~31.6 1.08~5.50 0.29~2.09 0.03~8.65
黄河中游 345 34.5~5980 0.08~480 0.26~3.79 0.18~3.33 0.06~0.91
黄河下游 2139 23.1~14700 0.23~528 0.50~8.00 0.37~3.33 0.03~0.32
渭河下游 155 21.0~3180 0.31~721 0.45~4.14 0.34~2.79 0.03~0.71
长江干支流 150 12.9~46600 0.01~4.42 0.85~18.7 0.07~2.79 0.07~0.30
— 1 5 2 —
0