Page 112 - 2023年第54卷第12期

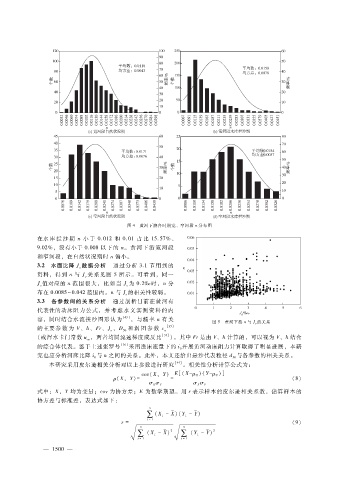
图 ４ 黄河下游各时期宽、窄河段 ｎ分布图

在水 库 拦 沙 期 ｎ小 于 ０．０１２和 ０．０１占 比 １５．５７％、
９．０２％，没有小于 ０．００８以下的 ｎ。黄河下游宽河段
和窄河段，在自然状况期时 ｎ偏小。
３．２ 水面比降 Ｊ数据分析 通过分析 ３．１节用到的
ｏ
资料，得到 ｎ与 Ｊ关系见图 ５所示。可看到，同一
ｏ
Ｊ值对应的 ｎ范围很大，比如当 Ｊ为 ０．２‰时，ｎ分
ｏ
ｏ
布在 ０．００８５～０．０４２范围内。ｎ与 Ｊ的相关性较弱。
ｏ
３．３ 各参数间的关系分析 通过剖析目前在黄河有
代表性的动床阻 力公 式，并考虑 水文 实测 资 料的内
容，同时结合水流挟沙图形认为 ［４３］ ，与糙率 ｎ有关
图 ５ 黄河下游 ｎ与 Ｊ ｏ 的关系
的主要参 数 为 Ｖ、ｈ、Ｆｒ、Ｊ、Ｄ 和 涡 团 参 数 ｃ ［３５］
ｏ ５０ ｎ
，两者均同流速梯度成反比 ［３３］ ）。其中 Ｆｒ是由 Ｖ、ｈ计算的，可以视为 Ｖ、ｈ结合
（或浑水卡门常数 κ ｍ
的综合体代表。鉴于上述张罗号 ［３６］ 采用造床流量下的 ｉ开展黄河动床阻力计算取得了明显进展，本研
０
究也应分析河床比降 ｉ与 ｎ之间的关系。此外，本文还给出悬沙代表粒径 ｄ 与各参数的相关关系。
０ ５０
本研究采用皮尔逊相关分析对以上参数进行研究 ［４４］ 。相关性分析计算公式为：
）］
ｃｏｖ （Ｘ，Ｙ） Ｅ［（Ｘ － μ Ｘ ）（Ｙ － μ Ｙ
ρ （Ｘ，Ｙ） ＝ ＝ （８）
σ Ｘ σ Ｙ σ Ｘ σ Ｙ
式中：Ｘ，Ｙ均为变量；ｃｏｖ为协方差；Ｅ为数学期望。用 ｒ表示样本的皮尔逊相关系数，估算样本的
协方差与标准差，表达式如下：
ｎ
Ｘ）（Ｙ －珔
∑ （Ｘ －珔 ｉ Ｙ）
ｉ
ｉ ＝１
ｒ ＝ （９）
ｎ ２ ｎ ２
∑
∑
Ｙ）
Ｘ）
槡 （Ｘ －珔 槡 （Ｙ －珔
ｉ
ｉ
ｉ ＝１
ｉ ＝１
０
— １ ５ ０ —