Page 113 - 2023年第54卷第12期

式中：ｎ为整个时间序列中的样本总数；ｉ代表样本数据的索引；Ｘ，Ｙ 分别为所选两个时间序列的第
ｉ ｉ
ｉ个样本； 珔 珔
Ｘ，Ｙ分别为两组时间序列的平均值。皮尔逊相关分析结果的值在 － １和 １之间。－ １和 １的
值都代表极致完美的线性相关，正数和负数分别表示正相关和负相关关系。另一种极端情况，即皮尔
逊相关分析值为 ０，意味着测试时间序列之间没有线性相关性。
本研究用来进行分析的黄河下游 ９９１组实测数据特征参数范围为：糙率的范围为 ０．００４～０．０５９；
３
含沙量 Ｓ为 ０．３４～５２８ｋｇ?ｍ ；Ｄ 为 ０．０２９～０．３２３ｍｍ。通过计算分析给出各变量间的相关关系如图 ６
５０
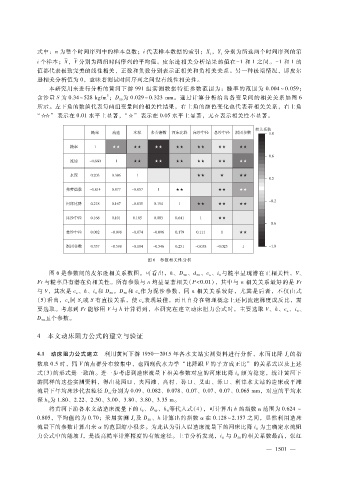
所示。左下角的数值代表每两组变量间的相关性结果，右上角的颜色变化也代表着相关关系，右上角
“ ☆☆” 表示在 ０．０１水平上显著，“ ☆” 表示在 ０．０５水平上显著，无☆表示相关性不显著。

图 ６ 参数相关性分析
图 ６是参数间的皮尔逊相关系数图。可看出，ｈ、Ｄ 、ｄ 、ｃ、ｉ与糙率呈现潜在正相关性，Ｖ、
ｎ
０
５０
５０
Ｆｒ与糙率具有潜在负相关性。所有参数与 ｎ均呈显著相关（Ｐ＜０．０１），其中与 ｎ相关关系最好的是 Ｆｒ
与 Ｖ，其次是 ｃ、ｈ、ｉ和 Ｄ 。Ｄ 和 ｃ作为泥沙参数，同 ｎ相关关系较好，尤其是后者，不仅由式
ｎ ０ ５０ ５０ ｎ
（ ５）看出，ｃ同 Ｓ或 Ｓ有直接关系，使 ｃ表现最佳，而且自身在物理概念上还同流速梯度成反比，需
ｎ
ｎ
ｖ
要选取。考虑到 Ｆｒ能够用 Ｖ与 ｈ计算得到，本研究在建立动床阻力公式时，主要选取 Ｖ、ｈ、ｃ、ｉ、
ｎ
０
Ｄ 五个参数。
５０
４ 本文动床阻力公式的建立与验证
４．１ 动床阻力公式建立 利用黄河下游 １９５０—２０１５年各水文站实测资料进行分析，水面比降 Ｊ的指
ｏ
数取 ０．５时，同 Ｖ的点群分布较集中，也同现代水力学 “比降跟 Ｖ的平方成正比” 的关系式以及上述
式（ ３）的形式是一致的。进一步考虑到造床流量下相关参数对应的河床比降 ｉ颇为稳定，统计黄河下
０
游同样的这些实测资料，得出花园口、夹河滩、高村、孙口、艾山、泺口、利津水文站的造床或平滩
流量下年均床沙代表粒径 Ｄ 分别为 ０．０９、０．０８２、０．０７８、０．０７、０．０７、０．０７、０．０６５ｍｍ，对应的平均水
ｍ
深 ｈ为 １．８０、２．２２、２．５０、３．００、３．８０、３．８０、３．３５ｍ。
０
将黄河下游各水文站造床流量下的 ｉ、Ｄ 、ｈ等代入式（４），可计算出 ｈ的指数 α范围为 ０．６２４～
０
０
５０
０．８０５ ，平均值约为 ０．７０；采用实测 Ｊ及 Ｄ 、ｈ计算出的指数 α在 ０．１２８～２．１５７之间，显然利用造床
５０
ｏ
流量下的参数计算出来 α的范围缩小很多。为此认为引入以造床流量下的河床比降 ｉ为主确定水流阻
０
力公式中的能坡 Ｉ，是提高糙率计算精度的有效途径。上节分析发现，ｉ与 Ｄ 的相关系数最高，张红
０ ５０
— １ ０ １ —
５