Page 111 - 2023年第54卷第12期

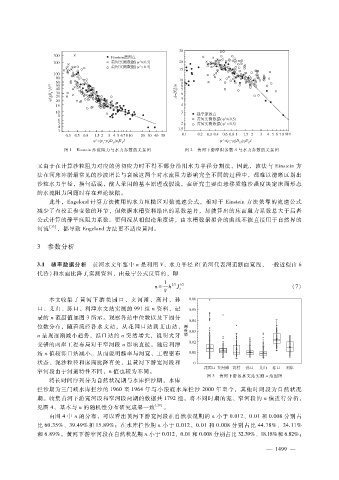
图 １ Ｅｉｎｓｔｅｉｎ沙波阻力与水力参数的关系图 图 ２ 黄河下游摩阻参数 Ａ与水力参数的关系图

又由于在计算沙粒阻力对应的剪切应力时不得不部分沿用水力半径分割法，因此，该法与 Ｅｉｎｓｔｅｉｎ方
法在河床冲淤最常见的沙波增长与衰减这两个对水流阻力影响完全不同的过程中，都难以清晰区划出
沙粒水力半径，换句话说，前人采用的基本原理或假说，在研究主要由悬移质输沙强度决定床面形态
的水流阻力问题时存在理论缺陷。
此外，Ｅｎｇｅｌｏｎｄ计算方法使用的水力粗糙区对数流速公式，相对于 Ｅｉｎｓｔｅｉｎ方法依靠的流速公式
减少了查校正参变数的环节，但依据水槽资料给出的系数差异，却使算出的床面阻力系数总大于后者
公式计算的静平床阻力系数。更何况从相似论角度讲，由水槽数据拟合的曲线不能直接用于自然界的
河流 ［３３］ ，都导致 Ｅｎｇｅｌｏｎｄ方法更不适应黄河。

３ 参数分析

３．１ 糙率数据分析 黄河水文年鉴中 ｎ是利用 Ｖ、水力半径 Ｒ（黄河代表河道断面宽浅，一般近似由 ｈ
代替）和水面比降 Ｊ实测资料，由曼宁公式反算的，即
ｏ
１
２?３ １?２
ｎ ＝ ｈ Ｊ （７）
ｏ
Ｖ
本文收集 了 黄 河 下 游 花 园 口、夹 河 滩、高 村、孙
口、艾山、泺口、利津水文站实测的 ９９１组 ｎ资料，记
录的 ｎ范围值如图 ３所示。观察各站中位数以及下四分
位数分布，随着流经各水文站，从花园口站到艾山站，
ｎ呈现逐渐减小趋势，泺口站的 ｎ突然增大，说明犬牙
交错的两岸工程布局对于窄河段 ｎ影响直接。随后利津
站 ｎ值较泺口站减小。从而说明糙率与河宽、工程密布
状态、泥沙粒径和床面比降有关，且黄河下游宽河段和
窄河段由于河道特性不同，ｎ值也较为不同。
图 ３ 黄河下游各水文站实测 ｎ范围图
将长时间序列分为自然状况期与水库拦沙期，水库
拦沙期为三门峡水库拦沙的 １９６０至 １９６４年与小浪底水库拦沙 ２０００年至今，其他时间段为自然状况
期。收集黄河下游宽河段和窄河段两期的数据共 １７９２组，将不同时期的宽、窄河段的 ｎ值进行分析，
见图 ４，基本与 ｎ的随机性分布研究成果一致 ［２９］ 。
由图 ４中 ｎ的分布，可以看出黄河下游宽河段在自然状况期的 ｎ小于 ０．０１２、０．０１和 ０．００８分别占
比 ６０．３５％、３９．４９％和 １５．８９％；在水库拦沙期 ｎ小于 ０．０１２、０．０１和 ０．００８分别占比 ４４．７８％、２４．１１％
和 ６．８９％。黄河下游窄河段在自然状况期 ｎ小于 ０．０１２、０．０１和 ０．００８分别占比 ３２．３９％、１８．１８％和 ６．８２％；

４
— １ ９ ９ —