Page 95 - 2024年第55卷第2期
P. 95
结得到的经验公式,易于计算且包含远场特征,被广泛采用 [27 - 30] 。因此,本文采用中国水科院经验公
式法初步分析坝前的涌浪高分布规律。
中国水科院经验公式中认为滑坡涌浪的高度与距滑坡体的距离、滑坡速度和滑坡体的体积有关。
距滑坡体不同距离的涌浪高度公式为:
n
v
H = k U 0.5 (1)
1
2g
k= { 0 .5,L ≤35.0 (2)
1
- 0.5945
6.1274L
,L>35.0
3
式中:H为距滑坡体 L处的滑坡涌浪高度,m;v为滑坡速度,m?s;U为滑坡体入水体积,m ;g为
2
重力加速度,g = 9.8m?s ;n为计算系数,n = 1.3~1.5 ;k为与距离 L有关的影响系数。
1
假设滑坡从左岸滑入水中,如图 2(b)所示,入水点到 31个坝段的距离分别记为 L,L,…,L ,
1 2 31
从而可以计算出 31个坝段的涌浪高度。
鉴于本文主要目的是研究不同的坝前滑坡涌浪分布规律对震损拱坝坝体损伤的影响。为了具有可
比性,经过前期的模拟试验,本文假定 31个坝段的坝前最大涌浪高相同,均为 100m。相应的中国水
3
8
7
科院经验公式中各个参数的计算范围设定为:L= 0.5~10km ,v = 10~100m?s ,U= 1 × 10~2 × 10 m 。
1
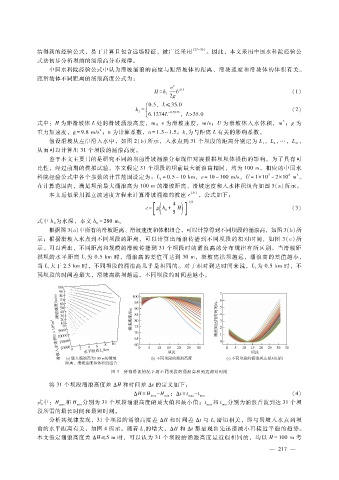
在计算范围内,满足坝前最大涌浪高为 100m的滑坡距离、滑坡速度和入水体积组合如图 3(a)所示。
[31]
本文近似采用孤立波速度方程来计算滑坡涌浪的波速 c ,公式如下:
( [ 4 )] 1?2
c = gh+ H (3)
0
5
式中 h为水深,本文 h= 280m。
0 0
根据图 3(a)中所有的滑坡距离、滑坡速度和体积组合,可以计算得到不同坝段的涌浪高,如图 3(b)所
示;根据滑坡入水点到不同坝段的距离,可以计算出涌浪传播到不同坝段的相对时间,如图 3(c)所
示。可以看出,不同距离和规模的滑坡传播到 31个坝段时的涌浪高的分布规律有所区别。当滑坡距
拱坝的水平距离 L为 0.5km时,涌浪高的差值可达到 30m,滑坡离拱坝越远,涌浪高的差值越小,
1
当 L大于 2.5km时,不同坝段的涌浪高几乎是相同的。对于相对到达时间来说,L为 0.5km时,不
1 1
同坝段的时间差最大,滑坡离拱坝越远,不同坝段的时间差越小。
图 3 所有滑坡情况下的不同坝段的涌浪高和到达相对时间
将 31个坝段涌浪高度差 Δ H和时间差 Δ t的定义如下:
Δ H = H - H ;Δ t = t - t (4)
max
min
max
min
式中:H 和 H 分别为 31个坝段涌浪高度的最大值和最小值;t 和 t 分别为涌浪首波到达 31个坝
max min max min
段所需的最长时间和最短时间。
分析其规律发现,31个坝段的涌浪高度差 Δ H和时间差 Δ t与 L密切相关,即与滑坡入水点到坝
1
前的水平距离有关,如图 4所示。随着 L的增大,Δ H和 Δ t都呈现出先迅速减小再接近平稳的趋势。
1
本文假定涌浪高度差 Δ H ≤5m时,可以认为 31个坝段的涌浪高度是近似相同的,均以 H= 100m考
— 2 1 7 —