Page 96 - 2024年第55卷第2期

虑；假定涌浪时间差 Δ ｔ ≤３ｓ时，不考虑其时间差，即认
为此时涌浪首波同时到达 ３１个坝段。因此，可以根据滑
坡入水点距坝址的水平距离分为三种情况：
Ｌ：０．５ｋｍ ≤Ｌ＜２．５ｋｍ，此时 ３１个坝段同时存在涌
１
Ａ
浪高度差和时间差；
Ｌ：２．５ｋｍ ≤Ｌ＜６．５ｋｍ，此时 ３１个坝段不存在高度
Ｂ
１
差，仅存在时间差；
Ｌ：Ｌ≥６．５ｋｍ，此时 ３１个坝段可以认为是同时作
Ｃ １
用均匀的涌浪高度。
基于上述分析，本文选出 ３种典型震后的滑坡涌浪
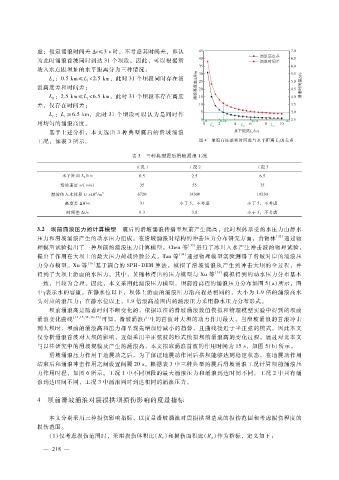
工况，如表 ３所示。 图 ４ 涌浪高度差和时间差与水平距离 Ｌ １ 的关系

表 ３ 三种典型震后滑坡涌浪工况
工况 １ 工况 ２ 工况 ３
水平距离 Ｌ １ ?ｋｍ ０．５ ２．５ ６．５
滑坡速度 ｖ?（ｍ?ｓ） ３５ ５５ ７５
４
滑坡体入水体积 Ｕ!１０?ｍ ３ ６７２０ １４３００ １９２３０
高度差 Δ Ｈ?ｍ ３１ 小于 ５，不考虑 小于 ５，不考虑
时间差 Δ ｔ?ｓ ６．３ ３．８ 小于 ３，不考虑

３．２ 坝前涌浪压力的计算模型 震后的滑坡涌浪传播至坝前产生爬高，此时坝体承受的水压力由静水
压力和滑坡涌浪产生的动水压力组成。在滑坡涌浪对结构的冲击压力分布研究方面，黄锦林 ［３２］ 通过物
理模型试验提出了一种坝前的涌浪压力计算模型。Ｃｈｅｎ等 ［３３］ 进行了冰川入水产生冲击波的物理试验，
提出了作用在大坝上的最大压力荷载经验公式。Ｔａｎ等 ［３４］ 通过物理模型实验测得了滑坡对岸的涌浪压
力分布模型。Ｘｕ等 ［１６］ 基于耦合的 ＳＰＨ － ＤＥＭ 算法，模拟了滑坡涌浪从产生到冲击大坝的全过程，并
得到了大坝上游面的水压力。其中，黄锦林得出的压力模型与 Ｘｕ等 ［１６］ 模拟得到的动水压力分布基本
一致，且较为合理。因此，本文采用此涌浪压力模型，坝前沿高程的涌浪压力分布如图 ５（ａ）所示，图
中"表示水的容重。在静水位以下，坝体上游面的涌浪压力沿高程是相同的，大小为 １．９倍的涌浪高水
头对应的浪压力；在静水位以上，１．９倍浪高范围内的涌浪压力采用静水压力分布形式。
坝前涌浪高是随着时间不断变化的，依据以往的滑坡涌浪数值模拟和物理模型实验中得到的坝前
涌浪变化曲线 ［１４，１５，３２，３５ － ３７］ 可知，滑坡涌浪产生的首波对大坝的动力作用最大，当滑坡涌浪的首浪冲击
到大坝时，坝前的涌浪高和压力都呈现先增加后减小的趋势，且曲线接近于半正弦的模式。因此本文
仅分析涌浪首波对大坝的影响，近似采用半正弦波的形式模拟坝前涌浪高的变化过程。通过对比本文
与以往研究中的滑坡规模及产生的涌浪高，本文拟取涌浪首波的作用时间为 １５ｓ，如图 ５（ｂ）所示。
滑坡涌浪压力作用于地震动之后，为了保证地震动作用后拱坝能够达到稳定状态，在地震动作用
结束后和涌浪冲击作用之间设置间隔 ２０ｓ。根据表 ３中三种典型的震后滑坡涌浪工况计算坝前涌浪压
力作用时程，如图 ６所示。工况 １中不同坝段的最大涌浪压力和涌浪到达时间不同，工况 ２中只有涌
浪到达时间不同，工况 ３中涌浪同时到达相同的涌浪压力。

４ 坝前滑坡涌浪对震损拱坝损伤影响的度量指标

本文分别采用三种损伤影响指标，以度量滑坡涌浪对震损拱坝造成的损伤范围和考虑损伤程度的
损伤范围。
（ １）仅考虑损伤范围时，采用损伤体积比（Ｒ）和损伤面积比（Ｒ）作为指标，定义如下：
Ｖ Ａ
８
— ２ １ —