Page 127 - 2024年第55卷第4期

为 ８４７ｍ，下游水位设置为 ７８０ｍ。模型中坝料物理力学参数取值见表 ５。模型共设置 １００万个网格单
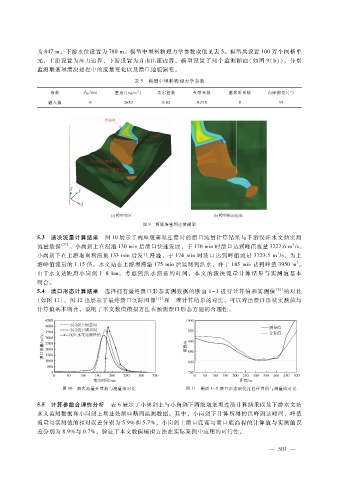
元，上游设置为压力边界，下游设置为自由出流边界。模型设置了两个监测断面（如图 ９（ｂ）），分别
监测堰塞坝溃决过程中的流量变化以及溃口地貌演变。
表 ５ 模型中坝料物理力学参数

３
参数 ｄ ５０ ?ｍｍ 重度?（ｋｇ?ｍ ） 希尔兹数 夹带系数 推移质系数 内摩擦角?（ !）
输入值 ９ ２６５０ ０．０２ ０．０１８ ８ ３５

图 ９ 两级堰塞坝连溃模型

５．３ 溃决流量计算结果 图 １０展示了两座堰塞坝连溃时的溃口流量计算结果与下游汉旺水文站实测
３
流量数据 ［３２］ 。小岗剑上在漫溢 １３０ｍｉｎ后溃口快速发展，于 １７０ｍｉｎ时溃口达到峰值流量 ３２２７．６ｍ ?ｓ。
３
小岗剑下在上游堰塞坝漫顶 １３３ｍｉｎ后发生漫溢，于 １７４ｍｉｎ时溃口达到峰值流量 ３７２３．５ｍ ?ｓ，为上
３
游峰值流量的 １．１５倍。水文站在上游坝漫溢 １７５ｍｉｎ后监测到洪水，并于 １８５ｍｉｎ达到峰值 ３９５０ｍ 。
由于水文站距离小岗剑上 ８ｋｍ，考虑到洪 水演进的 时间，本 文的 溃决 流量 计算 结果 与实 测 值基本
吻合。
５．４ 溃口形态计算结果 选择拥有最终溃口形态实测数据的断面 １ － １进行计算值和实测值 ［３２］ 的对比
（如图 １１），图 １２也展示了最终溃口实际图像 ［１３］ 和三维计算结果的对比，可以看出溃口形状实测值与
计算值基本吻合，说明了本文数值模拟方法在预测溃口形态方面的合理性。

图 １０ 溃决流量计算值与测量值对比 图 １１ 断面 １ － １溃口形态演化过程计算值与测量值对比

５．５ 计算参数合理性分析 表 ６展示了小岗剑上与小岗剑下两级堰塞坝连溃计算结果以及下游水文站
水文监测数据和小岗剑上坝址处溃口断面监测数据。其中，小岗剑下计算所得的洪峰到达时间、峰值
流量与实测值的相对误差分别为 ５．９％和 ５．７％，小岗剑上溃口底宽与溃口底高程的计算值与实测值误
差分别为 ８．９％与 ０．７％，验证了本文数值模拟方法在实际案例中应用的可行性。

— ５ ０ １ —