Page 36 - 2024年第55卷第4期

步骤 ３：根据精英策略，选择一部分非支配集 Ｚ中的个体，放入父代种群 Ｐ 。精英策略的目的
ｉ ＋ １
是保留优质解，防止解的优劣度下降。
步骤 ４：判断种群的大小是否满足设置条件。如果满足，进行交叉和变异操作来产生新的子代群
体 Ｑ 。交叉和变异是遗传算法中的常用操作，通过模拟自然界的遗传过程，产生新的解。如果种群
ｉ ＋ １
大小不满足条件，则将非支配集进行拥挤度排序，并重复步骤 ３。
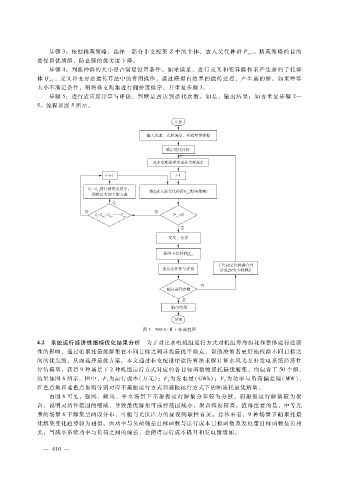
步骤 ５：进行适应度计算与评估，判断是否达到迭代次数。如是，输出结果；如否重复步骤 ２—
５。流程如图 ５所示。

图 ５ ＮＳＧＡ － Ⅱ工作流程图

４．２ 系统运行经济性指标优化结果分析 为了对比水电机组运行方式对机组寿命损耗和整体运行经济
性的影响，通过帕累托最优解集在不同目标之间寻找最优平衡点，帮助决策者更好地权衡不同目标之
间的优先级，从而选择最优方案。本文通过非支配排序遗传算法求解计算水风光互补发电系统经济性
评估模型，获得 ９种场景下 ２种机组运行方式对应的各目标函数帕累托最优解集，均包含了 ５０个解，
结果如图 ６所示。图中，Ｆ为运行成本（万元）；Ｆ为发电量（ＧＷｈ）；Ｆ为功率与负荷偏差值（ＭＷ），
１
２
３
红色点集和蓝色点集则分别对应不避振运行方式和避振运行方式下的帕累托最优解集。
由图 ６可见，强风、微风、平水场景下不避振运行解集分布较为分散，而避振运行解集较为聚
合，说明灵活性范围的缩减，导致最优解集可选择范围减小，聚合程度较高。值得注意的是，中等光
照的场景 ６下解集呈两段分布，可能与光伏出力的昼夜间歇性有关。总体来看，９种场景下帕累托最
优解集变化趋势较为相似。而功率与负荷偏差目标函数与运行成本目标函数及发电量目标函数呈负相
关，当减小系统功率与负荷之间的偏差，会使得运行成本提升和发电量增加。

０
— ４ １ —