Page 68 - 2024年第55卷第5期

４ 案例研究

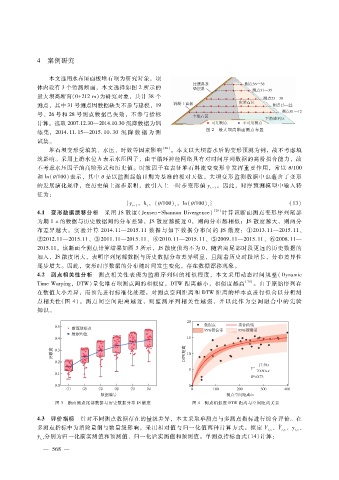
本文选用水布垭面板堆石坝为研究对象，坝
体内设有 ３个监测断面，本文选择如图 ２所示的
最大坝高断面（ ０ ＋ ２１２ｍ）为研究对象，共计 ３８个
测点，其中 ３１号测点因数据缺失不参与建模，１９
号、２６号和 ２８号测点数据已失效，不参与指标
计算。选取 ２００７．１２．３０—２０１４．１０．３０沉降数据为训
图 ２ 最大坝高断面测点布置
练集，２０１４．１１．１５—２０１５．１０．３０沉 降 数 据 为 测
试集。
堆石坝变形受填筑、水压、时效等因素影响 ［２８］ 。本文以大坝蓄水后的变形预测为例，故不考虑填
筑影响。采用上游水位 ｈ表示水压因子，由于循环神经网络具有对时间序列数据的高阶拟合能力，故
不考虑水压因子的高阶形式和历史值。时效因子在表征堆石料流变变形中发挥重要作用，常以 θ ?１００
和 ｌｎ（ θ ?１００）表示，其中 θ 是以监测起始日期为基准的相对天数。大坝变形监测数据中也蕴含了变形
的发展演化规律，在历史值上逐步累积，故引入上一时步变形值 ｙ 。因此，时序预测模型中输入特
ｔ － １
征为：
｛ｙ ，ｈ，（ θ ?１００），ｌｎ（ θ ?１００）｝ （１３）
ｔ － １ ｔ ｔ ｔ
４．１ 变形数据漂移分析 采用 ＪＳ散度（Ｊｅｎｓｅｎ － ＳｈａｎｎｏｎＤｉｖｅｒｇｅｎｃｅ） ［２９］ 计算该断面测点变形序列尾部
为期 １ａ的数据与历史数据间的分布差异，ＪＳ散度越接近 ０，则两分布越相似；ＪＳ散度越大，则两分
布差异 越 大。实 验计算 ２０１４．１１—２０１５．１１数 据与如下 数 据分 布 间 的 ＪＳ散 度：① ２０１３．１１—２０１５．１１、
②２０１２．１１—２０１５．１１、③２０１１．１１—２０１５．１１、④２０１０．１１—２０１５．１１、⑤２００９．１１—２０１５．１１、⑥２００８．１１—
２０１５．１１。该断面全测点计算结果如图 ３所示，ＪＳ散度值均不为 ０，随着离尾部时段更远的历史数据的
加入，ＪＳ散度增大，表明序列尾部数据与历史数据分布差异明显，且随着历史时段增长，分布差异性
逐步增大。因此，变形时序数据的分布随时间发生变化，存在数据漂移现象。
４．２ 测点相关性分析 测点相关性表现为监测序列间的相似程度，本文采用动态时间规整（Ｄｙｎａｍｉｃ
ＴｉｍｅＷａｒｐｉｎｇ ，ＤＴＷ）量化堆石坝测点间的相似度，ＤＴＷ 距离越小，相似度越高 ［３０］ 。由于原始序列存
在数值大小差异，需预先进行标准化处理。对测点空间距离和 ＤＴＷ 距离的样本点进行拟合以分析测
点相关性（图 ４）。测 点间 空 间 距 离 越 近，则 监 测 序 列 相 关 性 越 强，并 以 此 作 为 空 间 融 合 中 的 先 验
知识。

图 ３ 断面测点尾部数据与历史数据分布 ＪＳ散度 图 ４ 测点相似度 ＤＴＷ 距离与空间距离关系

４．３ 评价指标 针对不同测点数据存在的量级差异，本文采取单测点与多测点指标进行综合评价。在
＾
多测点指标中为消除量纲与数量级影响，采用相对值与归一化值两种计算方式。拟定 Ｙ 、Ｙ 、ｙ 、
ｉ，ｔ
ｉ，ｔ
ｉ，ｔ
＾ 分别为归一化前实测值和预测值、归一化后实测值和预测值。单测点指标由式（１４）计算：
ｙ
ｉ，ｔ
— ５ ６ —
８