Page 133 - 2025年第56卷第2期

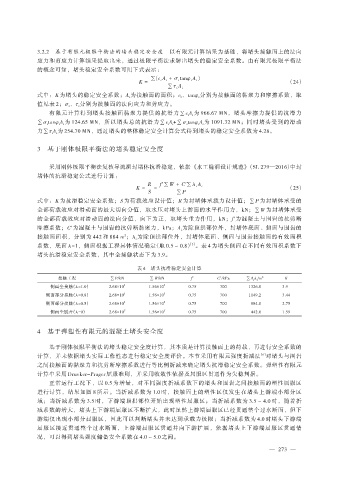
3.2.2 基于有限元极限平衡法的堵头稳定安全度 以有限元计算结果为基础，将堵头接触面上的法向
应力和剪应力计算结果提取出来，通过极限平衡法求解出堵头的稳定安全系数。由有限元极限平衡法
的概念可知，堵头稳定安全系数可用下式表示：
∑(c i A i + σ i tanφ i A i )
K = （24）
∑τ i A i
式中：K 为堵头的稳定安全系数；A 为接触面的面积；c 、tanφ 分别为接触面的黏聚力和摩擦系数，取
i
i
i
值见表 2；σ 、τ 分别为接触面的法向应力和剪应力。
i
i
有限元计算得到堵头接触面黏聚力提供的抗滑力∑c A 为 966.67 MN，堵头摩擦力提供的抗滑力
i
i
∑σ tanφ A 为 124.65 MN，所以堵头总的抗滑力∑c A +∑σ tanφ A 为 1091.32 MN；同时堵头受到的滑动
i
i
i
i
i
i
i
i
力∑τ A 为 254.70 MN，通过堵头的整体稳定安全计算公式得到堵头的稳定安全系数为 4.28。
i
i
3 基于刚体极限平衡法的堵头稳定安全度
采用刚体极限平衡法复核导流洞封堵体抗滑稳定，依据 《水工隧洞设计规范》（SL 279—2016）中封
堵体的抗滑稳定公式进行计算：
R f'∑W + C'∑λ i A i
K = = （25）
S ∑P
式中：K 为抗滑稳定安全系数；S 为荷载效应设计值；R 为封堵体承载力设计值；∑P 为封堵体承受的
全部荷载效应对滑动面的最大切向分值，取水压对堵头上游面的水平作用力，kN；∑W 为封堵体承受
的全部荷载效应对滑动面的法向分值，向下为正，取堵头重力作用，kN；f'为混凝土与围岩的抗剪断
摩擦系数；C'为混凝土与围岩的抗剪断黏聚力，kPa；A 为除顶拱部位外，封堵体底面、侧面与围岩的
i
接触面面积，分别为 442 和 884 m ；λ 为除顶拱部位外，封堵体底面、侧面与围岩接触面的有效面积
2
i
［3］
系数，底面 λ=1，侧面根据工程具体情况确定（取 0.5 ~ 0.8） 。表 4 为堵头侧面在不同有效面积系数下
堵头抗滑稳定安全系数，其中全接触状态下为 3.9。
表 4 堵头抗滑稳定安全计算
接触工况 ∑P/kN ∑W/kN f' C'/kPa ∑A λ /m 2 K
i i
侧面全接触（λ=1.0） 2.68×10 5 1.56×10 5 0.75 700 1326.0 3.9
侧面部分接触（λ=0.8） 2.68×10 5 1.56×10 5 0.75 700 1149.2 3.44
侧面部分接触（λ=0.5） 2.68×10 5 1.56×10 5 0.75 700 884.0 2.75
侧面全脱开（λ=0） 2.68×10 5 1.56×10 5 0.75 700 442.0 1.59

4 基于弹塑性有限元的混凝土堵头安全度

基于刚体极限平衡法的堵头稳定安全度计算，其本质是计算接触面上的荷载，再进行安全系数的
［6］
计算，并未依据堵头实际工作性态进行稳定安全度评价。本节采用有限元强度折减法 对堵头与围岩
之间接触面的黏聚力和抗剪断摩擦系数进行等比例折减来确定堵头抗滑稳定安全系数。弹塑性有限元
计算中采用 Drucker-Prager 屈服准则，并采用收敛性依据及屈服区贯通作为失稳判据。
正常运行工况下，以 0.5 为增量，对不同强度折减系数下的堵头和围岩之间接触面的塑性屈服区
进行计算，结果如图 8 所示。当折减系数为 1.0 时，接触面上的塑性区仅发生在堵头上游端小部分区
域；当折减系数为 3.5 时，下游端顶拱部位开始出现塑性屈服区；当折减系数为 3.5 ~ 4.0 时，随着折
减系数的增大，堵头上下游端屈服区不断扩大，此时虽然上游端屈服区已经贯通整个过水断面，但下
游端仅出现小部分屈服区，因此可以判断堵头并未达到承载力极限；当折减系数为 4.0 时堵头下游端
屈服区接近贯通整个过水断面，上游端屈服区贯通并向下游扩展，依据堵头上下游端屈服区贯通情
况，可以得到堵头强度储备安全系数在 4.0 ~ 5.0 之间。

— 273 —