Page 121 - 水利学报2025年第56卷第3期

ｏ＝ σ （Ｗ ·［ｈ ，ｘ］ ＋ ｂ） （１６）
ｔ ｏ ｔ － １ ｔ ｏ
ｈ＝ ｏ ⊙ｔａｎｈ（Ｃ） （１７）
ｔ ｔ ｔ
式中：ｈ 和 ｈ为上一时刻单元的输出和当前细胞的输出；Ｗ 、Ｗ 、Ｗ 、Ｗ 分别为各层相应的权重系
ｆ
ｉ
ｔ
ｔ － １
ｏ
ｃ
数；ｂ、ｂ、ｂ、ｂ分别为各层相应的偏置项；σ为 Ｓｉｇｍｏｉｄ函数；ｆ、ｉ、 珟 Ｃ、Ｃ、ｏ分别为遗忘门、
ｔ
ｃ
ｔ
ｏ
ｔ
ｔ
ｔ
ｉ
ｆ
输入门、当前时刻初始细胞状态、更新后的当前时刻细胞状态以及输出门的值；⊙为 ｈａｄａｍａｒｄ积。
在 ＬＳＴＭ网络中隐层神经元个数、最大训练次数、学习率为模型关键超参数，人为确定存在较大
不确定性且影响模型精度，通过 ＳＳＡ算法对以上超参数进行寻优可有效提高模型预测精度。
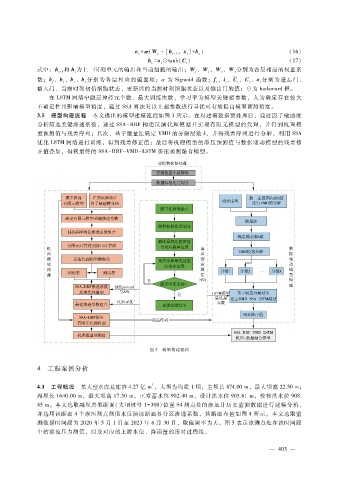
３．５ 模型构建流程 本文提出的模型建模流程如图 ３所示。在对建模数据预处理后，通过因子敏感度
分析筛选关键渗透系数，通过 ＳＳＡ － ＲＢＦ构建反演代理模型并实现有限元模型的代理，并得到机理模
型预测值与残差序列；其次，基于能量法确定 ＶＭＤ的分解层数 ｋ，并将残差序列进行分解，利用 ＳＳＡ
优化 ＬＳＴＭ网络进行训练，得到残差修正值；最后将机理模型的渗压预测值与数据驱动模型的残差修
正值叠加，得到最终的 ＳＳＡ － ＲＢＦ － ＶＭＤ － ＬＳＴＭ渗压预测融合模型。

图 ３ 模型构建流程

４ 工程案例分析

３
４．１ 工程概况 某大型水库总库容 ４．２７亿 ｍ ，大坝为均质土坝，主坝长 ８７４．００ｍ，最大坝高 ２２．５０ｍ；
副坝长 １６４０．００ｍ，最大坝高 １７．５０ｍ，正常蓄水位 ９０２．４０ｍ，设计洪水位 ９０３．６１ｍ，校核洪水位 ９０８．
４５ｍ。本文选取副坝典型断面（大坝桩号 １ ＋ ３００）位置 Ｓ４测点处的渗压计历史监测数据进行建模分析，
并选用该断面 ４个渗压测点测值来反演该断面各分区渗透系数，其断面布置如图 ４所示。本文选取监
测数据时间段为 ２０２０年 ５月 １日至 ２０２３年 ６月 ３０日，取值频率为天。图 ５表示该测点处在该时间段
中的渗流压力测值，以及对应的上游水位、降雨量的历时过程线。

— ４ ０ ３ —