Page 124 - 水利学报2025年第56卷第3期

基于反演结果构建 Ｓ４测点渗压预测代理模型。以上游水位作为输入，渗压测值作为输出，选取
９００．００ｍ至 ９０８．４５ｍ范围内的上游水位值与其对应的有限元计算结果作为训练数据建立模型，所选上
游水位范围涵盖了水库的特征水位，模型构建方法同反演代理模型一致。经多次寻优结果稳定不再变
化时，ＲＢＦ渗压预测代理模型的扩展速度和隐层神经元个数分别为 ｓｐｒｅａｄ ＝ １．０２６ ，ＭＮ＝ ５ 。根据计算
结果可知以该反演结果构建 Ｓ４测点处渗压预测代理模型，存在固有误差 ｅ ＝ ０．４５ｍ ，将其用于修正机
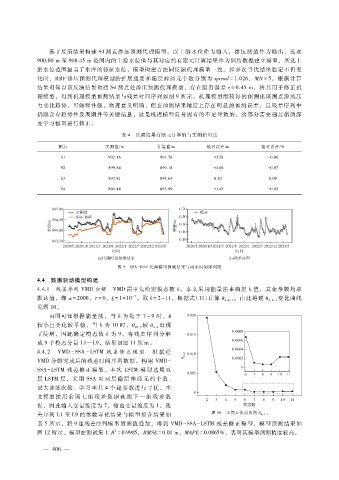
理模型，得到机理模型预测结果与残差时间序列如图 ９所示。机理模型能较好的预测出该测点渗流压
力变化趋势，可解释性强，物理意义明确，但在预测结果精度上存在明显的预测误差，且残差序列中
仍隐含有趋势性及周期性等关键信息，这是机理模型自身固有的不足导致的，这部分需要通过借助深
度学习模型进行修正。

表 ４ 反演结果有限元计算值与实测值对比

测点 实测值?ｍ 计算值?ｍ 绝对误差?ｍ 相对误差?％
Ｓ１ ９０２．１６ ９０１．５８ － ０．５８ － ０．０６
Ｓ２ ８９９．８４ ８９９．１８ － ０．６６ － ０．０７

Ｓ３ ８９３．８１ ８９４．６４ ０．８３ ０．０９
Ｓ４ ８９４．４４ ８９３．９９ － ０．４５ － ０．０５

图 ９ ＳＳＡ － ＲＢＦ代理模型预测结果与残差时间序列图

４．４ 数据驱动模型构建
４．４．１ 残差序列 ＶＭＤ分解 ＶＭＤ需事先给定模态数 ｋ，本文采用能量法来确定 ｋ值，其余参数均取
－ ７
默认值，即 α ＝ ２０００ ，τ ＝ ０ ，ξ ＝ １ × １０ 。取 ｋ ＝ ２～１１ ，根据式（１１）计算 θ ｋ，ｋ － １ 。由此得到 θ ｋ，ｋ － １ 变化曲线
见图 １０。
由图可知根据能量法，当 ｋ为处于 ７～９时，θ
出现
较小且变化较平稳，当 ｋ为 １０时，θ １０，９ 较 θ ９，８
了陡增，因此确定模态数 ｋ为 ９。将残差序列分解
成 ９个模态分量 Ｌ１—Ｌ９，结果如图 １１所示。
４．４．２ ＶＭＤ－ ＳＳＡ－ ＬＳＴＭ 残 差 修 正 模 型 根 据 经
ＶＭＤ分解完成后的残差时间序列数据，构建 ＶＭＤ －
ＳＳＡ － ＬＳＴＭ 残差修正模型。本次 ＬＳＴＭ 模型选用双
层 ＬＳＴＭ层，采 用 ＳＳＡ对 两层 隐 层 神 经 元 的 个 数、
最大训练次数、学习率共 ４个超参数进行寻优。本
文模型使 用 前 面 七 组 残 差 数 据 预 测 下 一 组 残 差 数
据，因此输入变量维度为 ７，输出变量维度为 １。残
差序列 Ｌ１至 Ｌ９的参数寻优结果与模型拟合结果如 图 １０ 不同 ｋ值对应的 θ ｋ，ｋ － １
表 ５所示，将 ９组残差序列模型预测值叠加，得到 ＶＭＤ － ＳＳＡ － ＬＳＴＭ 残差修正模型，模型预测结果如
２
图 １２所示。模型在测试集上 Ｒ ＝ ０．９９０５ ，ＲＭＳＥ ＝ ０．０１ｍ ，ＭＡＰＥ ＝ ０．０８６５％，表明其模型预测精度较高。

６
— ４ ０ —