Page 30 - 水利学报2025年第56卷第3期

定，通过加权得到调度预案的综合风险值，如下所示：
ｍ
ｉ ∑
ｍ ＝ ω ｊ ｉｊ （５）
ｎ
ｊ ＝１
为第 ｊ个指标的权重；ｎ为指标标准化后的规范值。
ｉ ｉｊ
式中：ｍ为对象 ｉ的综合风险值；ω ｊ
２．２．３ 基于云模型的调度预案综合风险分析 目前，防洪风险分析面临多重挑战，气候变化正导致极端
天气事件发生的频次和强度不断增加，快速的城市化和土地使用方式的变化也在加剧防洪风险，这使得
现有的传统评估方法难以适用。云模型是由李德毅 ［２７］ 院士在概率统计学和模糊集理论的基础上，提出的
一种可以完成定性概念与定量数值相互转换的模型，能综合考虑风险事件的模糊性、离散性与随机性。
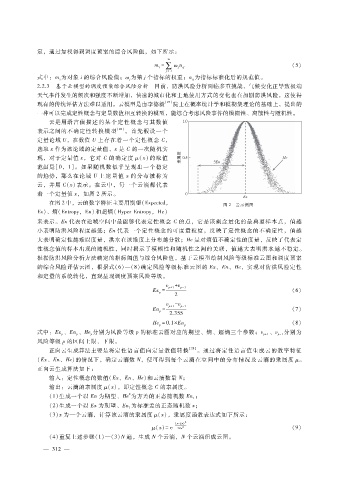
云是用语言值描述的 某个 定性概 念与 其数值
表示之间的不确定性转换模型 ［２８］ 。首先假设一个
定量论域 Ｕ，在数值 Ｕ上存在着一个定性概念 Ｃ，
选取 ｘ作为该论域的定量值，ｘ是 Ｃ的一次随机实
现，对于定量值 ｘ，它对 Ｃ的确定度 μ （ｘ）的取值
范围是［０，１］。如果随机数似乎呈现出一个稳定
的趋势，那么在论域 Ｕ上定量值 ｘ的分布被称为
云，并用 Ｃ（ｘ）表示。在云中，每一个云滴都代表
着一个定量值 ｘ，如图 ２所示。
在图 ２中，云的数字特征主要用期望（Ｅｘｐｅｃｔｅｄ，
图 ２ 云示例图
Ｅｘ）、熵（Ｅｎｔｒｏｐｙ，Ｅｎ）和超熵（ＨｙｐｅｒＥｎｔｒｏｐｙ，Ｈｅ）
来表示。Ｅｘ代表在论域空间中最能够代表定性概念 Ｃ的点，它是该概念量化的最典型样本点，值越
小表明防洪风险程度越低；Ｅｎ代表一个定性概念的可度量粒度，反映了定性概念的不确定性，值越
大表明确定性越难以度量，洪水在该维度上分布越分散；Ｈｅ是对熵值不确定性的度量，反映了代表定
性概念值的样本出现的随机性，同时揭示了模糊性和随机性之间的关联，值越大表明洪水越不稳定。
根据防洪风险分析方法确定的指标阈值与综合风险值，基于云模型绘制风险等级标准云图和调度预案
的综合风险评估云图，根据式（ ６）—（８）确定风险等级标准云图的 Ｅｘ、Ｅｎ、Ｈｅ，实现对防洪风险定性
和定量的系统转化，直观呈现调度预案风险等级。
ｖ ＋ ｖ
ｐ ＋ １
ｐ － １
Ｅｘ＝ （６）
ｐ
２
ｖ － ｖ
ｐ － １
ｐ ＋ １
Ｅｎ＝ （７）
ｐ
２．３５５
Ｈｅ＝ ０ ．１ × Ｅｎ ｐ （８）
ｐ
式中：Ｅｘ、Ｅｎ、Ｈｅ分别为风险等级 ｐ的标准云图对应的期望、熵、超熵三个参数；ｖ 、ｖ 分别为
ｐ ｐ ｐ ｐ ＋ １ ｐ － １
风险等级 ｐ的区间上限、下限。
正向云生成算法主要是将定性语言值向定量数值转换 ［２８］ 。通过将定性语言值生成云的数字特征
（Ｅｘ、Ｅｎ、Ｈｅ）的情况下，确定云滴数 Ｎ，便可得到每个云滴在空间中的分布情况及云滴的隶属度 μ 。
正向云生成算法如下：
输入：定性概念的数值（Ｅｘ、Ｅｎ、Ｈｅ）和云滴数量 Ｎ；
输出：云滴的隶属度 μ （ｘ），即定性概念 Ｃ的隶属度。
２
（ １）生成一个以 Ｅｎ为期望、Ｈｅ为方差的正态随机数 Ｅｎ；
１
（ ２）生成一个以 Ｅｘ为期望、Ｅｎ为标准差的正态随机数 ｘ；
１
（３）ｘ为一个云滴，计算该云滴的隶属度 μ （ｘ），隶属度函数表达式如下所示：
（ｘ － Ｅｘ） ２
－
μ （ｘ） ＝ｅ ２Ｅｎ ２ （９）
（４）重复上述步骤（１）—（３）Ｎ遍，生成 Ｎ个云滴，Ｎ个云滴组成云图。

— ３ １ —
２