Page 62 - 水利学报2025年第56卷第4期

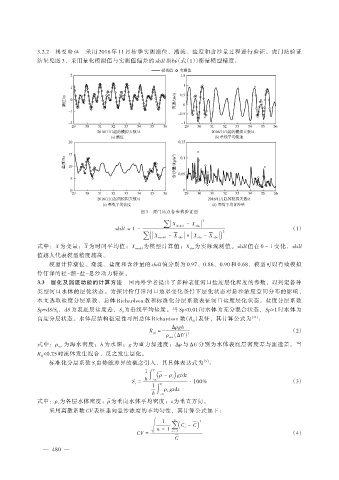
3.2.2 模型验证 采用 2016 年 11 月枯季实测潮位、潮流、盐度和含沙量过程进行验证。虎门站验证
结果见图 3，采用量化模拟值与实测值偏差的 skill 指标（式（1））衡量模型精度：

图 3 虎门站点各参数验证图
| 2
∑( | X model - X obs | + | X obs - X obs | ) 2
skill = 1 - ∑ | X model - X obs （1）
-
-
-
式中：X 为变量；X 为时间平均值；X 为模型计算值；X 为实际观测值。skill 值在 0 ~ 1 变化，skill
model obs
值越大代表模型精度越高。
模型计算潮位、潮流、盐度和含沙量的 skill 值分别为 0.97、0.86、0.90 和 0.68，模型可以有效模拟
伶仃洋的径-潮-盐-悬沙动力特征。
3.3 层化及湍流动能的计算方法 国内外学者提出了多种表征河口盐度层化程度的参数，以判定各种
类型河口水体的层化状态。为探讨伶仃洋河口地形变化条件下层化状态对悬沙浓度空间分布的影响，
本文选取盐度分层系数、总体 Richardson 数和标准化分层系数表征河口盐度层化状态。盐度分层系数
Sp=dS/S ，dS 为表底层盐度差，S 为垂线平均盐度。当 Sp<0.01 时水体为充分混合状态，Sp>1 时水体为
0 0
高度分层状态。水体层结构稳定性可用总体 Richardson 数（R ）表征，其计算公式为 ［24］ ：
i0
Δρgh
R i0 = - （2）
ρ sea (ΔU ) 2
式中：ρ 为海水密度；h 为水深；g 为重力加速度；Δρ 与 ΔU 分别为水体表底层密度差与流速差。当
sea
R <0.25 时流体发生混合，反之发生层化。
i0
［5］
标准化分层系数 S 由势能差异的概念引入，其具体表达式为 ：
r
0
1 ∫ ( - )
ρ - ρ i gzdz
h -h
S r = ⋅ 100% （3）
1 0 ρ i gzdz
h ∫ -h
-
式中：ρ i 为各层水体密度；ρ 为垂向水体平均密度；z 为垂直方向。
采用离散系数 CV 表征垂向悬沙浓度的不均匀性，其计算公式如下：
∑( C i - C ) 2
1 n -
n - 1
-
CV = i = 1 （4）
C
— 480 —