Page 48 - 2021年第52卷第7期

数法 ［29］ 、Brown-Forsythe 法 ［30］ 等检测序列的跳跃点；采用分段趋势相关系数识别法 ［31］ 、过程线法、
Kendall 检验法 ［32］ 等鉴别趋势成分；采用滑动周期相关系数识别法 ［33］ 、周期图法、最大熵谱分析法 ［34-35］
等检验序列的周期成分。
显著性水平分别选取 α = 0.05、β = 0.01 ， 表 7 实测径流序列变异诊断结果
对以上序列进行变异诊断分析 ［36］ ，其中结果
站点 变异诊断结果
如表 7 所示。结果表明，花园口站的年径流 花园口站 跳跃（1932）
序列在 1932 年发生了明显的跳跃变异，这主 汉口站 周期（12a）
要是气候变异直接导致的 ［37］ ；汉口站的月径 沙市站 周期（12a）
流序列和沙市站的月径流序列都存在 12 a 的
周期变异，这种周期波动现象主要和区域的气候条件及水文地理特征密切相关 ［24］ 。
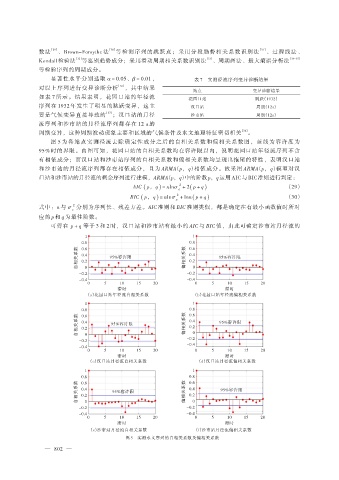
图 5 为各站点实测径流去除确定性成分之后的自相关系数和偏相关系数图，蓝线为容许度为
95％时的界限。由图可知，花园口站的自相关系数均在容许限以内，说明花园口站年径流序列不含
有相依成分；而汉口站和沙市站序列的自相关系数和偏相关系数均呈现出拖尾的特性，表明汉口站
和沙市站的月径流序列都存在相依成分，且为 ARMA（p，q）相依成分。故采用 ARMA（p，q）模型对汉
口站和沙市站的月径流的剩余序列进行建模，ARMA（p，q）中的阶数 p，q运用 AIC与 BIC准则进行判定：
)
AIC ( p，q = nlnσ + 2( p + q ) （29）
2
ε
)
BIC ( p，q = nlnσ + lnn( p + q ) （30）
2
ε
式中：n 与 σ 分别为序列长、残差方差。AIC 准则和 BIC 准则类似，都是确定在有最小函数值时所对
2
ε
应的 p 和 q 为最佳阶数。
可得在 p + q 等于 3 和 2 时，汉口站和沙市站有最小的 AIC 与 BIC 值，由此可确定沙市站月径流的
1 1
0.8 0.8
自相关系数 0.4 95%容许限 偏相关系数 0.4 95%容许限
0.6
0.6
0.2
0.2
-0.2 0 -0.2 0
-0.4 -0.4
0 5 10 15 20 0 5 10 15 20
滞时 滞时
（a）花园口站年径流自相关系数 （b）花园口站年径流偏相关系数
1 1
0.8 0.8
自相关系数 0.4 95%容许限 偏相关系数 0.4 95%容许限
0.6
0.6
0.2
0.2
0
-0.2 0
-0.2
-0.4
-0.4
0 5 10 15 20 0 5 10 15 20
滞时 滞时
（c）汉口站月径流自相关系数 （d）汉口站月径流偏相关系数
1 1
0.8 0.8
自相关系数 0.4 95%容许限 偏相关系数 0.4 95%容许限
0.6
0.6
0.2
0.2
-0.2 0 -0.2 0
-0.4 -0.4
0 5 10 15 20 0 5 10 15 20
滞时 滞时
（e）沙市站月径流自相关系数 （f）沙市站月径流偏相关系数
图 5 实测水文序列的自相关系数及偏相关系数
— 802 —