Page 46 - 2021年第52卷第7期

显著性水平中选取第一显著性水平 α =0.05、第二显著性水平 β =0.01；然后根据相依变异程度分级
表（即表 1）中各个变异等级对应的相关系数 r 的取值范围，并结合所提水文相依变异分级方法的理论
1 - ρ φ - ρ φ - ⋯ - ρ φ
基础式（19），求取各相依变异程度所对应的整体变量 H = 1 1 2 2 p p 的取值区间；最后
1 + θ + θ + ⋯ + θ 2
2
2
1 2 q
选取满足整体变量 H 在取值区间内的系数值组合，生成具有相依变异成分的模拟序列。下面仍以 AR⁃
MA（1， 1）和 ARMA（1， 2）模 型 为 例 进 行 验 证 。 纯 随 机 成 分 在 模 拟 序 列 中 的 长 度 n = 100 、 均 值
u = 100 、变差系数 C = 0.2 、偏态系数 C = 0.4 ，且服从 P - Ⅲ 型分布。
vu
su
3.3.1 ARMA（1，1）模型 在 ARMA（1，1）模型中，它的自回归部分和滑动平均部分的阶数分别为
1 - φ 2
p = 1、q = 1 ，根据式（22）—（24）可知此时整体变量 H 可表示为 H = 1 。各相依变异程度对应的整
1 + θ 2
1
体变量 H 的取值区间见表 5。

表 5 ARMA（1，1）模型各相依变异程度区间所对应的整体变量 H 的取值范围
1 - φ 2
H = 1 取值范围 相关系数 r 取值范围 相依变异程度
1 + θ 2
1
（0.9401，1.0000］ ［0.0000，0.2447） 无变异
（0.9094，0.9401］ ［0.2447，0.3010） 弱变异
（0.6400，0.9094］ ［0.3010，0.6000） 中变异
（0.3600，0.6400］ ［0.6000，0.8000） 强变异
（0.0000，0.3600］ ［0.8000，1.0000） 巨变异
在上述条件下，分别选取一阶自回归与一阶滑动平均 φ = 0.12、θ = 0.10 ， φ = 0.20、θ = 0.16 ，
1 1 1 1
φ = 0.25、θ = 0.24， φ = 0.50、θ = 0.70 和 φ = 0.80、θ = 0.95 共 5 组系数值，由这 5 组系数值求得的
1 1 1 1 1 1
整体变量 H 分别对应相依变异程度的 5 个等级。模拟生成这 5 种情形下的序列，绘于图 3，并计算出
所生成序列与其相依成分之间的相关系数。
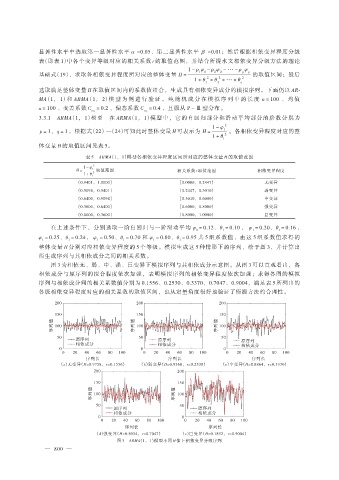
图 3 为相依无、弱、中、强、巨变异下模拟序列与其相依成分示意图。从图 3 可以直观看出，各
相依成分与原序列的拟合程度依次加强，表明模拟序列的相依变异程度依次加强；求得各图的模拟
序列与相依成分间的相关系数值分别为 0.1556、0.2530、0.3370、0.7047、0.9004，满足表 5 所列出的
各级相依变异程度对应的相关系数的取值区间，也从定量角度很好地验证了所提方法的合理性。

200 200 200

150 150 150
序列值 100 序列值 100 序列值 100

50 原序列 50 原序列 50 原序列
相依成分 相依成分 相依成分
0 0 0
0 20 40 60 80 100 0 20 40 60 80 100 0 20 40 60 80 100
序列长 序列长 序列长
（a）无变异（H=0.9758，r=0.1556） （b）弱变异（H=0.9360，r=0.2530） （c）中变异（H=0.8864，r=0.3370）
200 200

150 150
序列值 100 序列值 100

50 50
原序列 原序列
相依成分 相依成分
0 0
0 20 40 60 80 100 0 20 40 60 80 100
序列长 序列长
（d）强变异（H=0.5034，r=0.7047） （e）巨变异（H=0.1892，r=0.9004）
图 3 ARMA（1，1）模型不同 H 值下相依变异分级序列
— 800 —