Page 45 - 2021年第52卷第7期

P-Ⅲ型分布，其长度 n = 1000 、均值 u = 100 、变差系数 C = 0.2 、偏态系数 C = 0.4 。为单独研究
vu
su
两种待定系数的影响，选取两组 φ 、θ 值。第一组滑动平均系数 θ 取固定值 0.2，自回归系数分别取
1 1 1
φ = -0.9、 - 0.5和 - 0.2 ； 第 二 组 自 回 归 系 数 φ 取 固 定 值 0.2， 滑 动 平 均 系 数 分 别 取
1 1
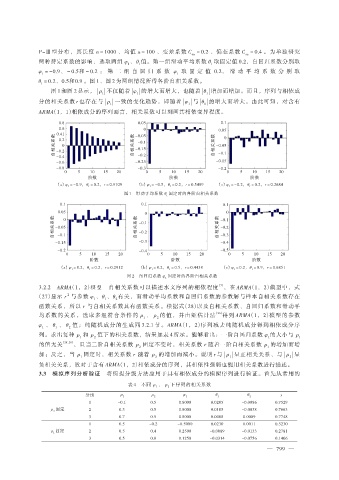
θ = 0.2、0.5和0.9 。图 1、图 2 为两组情况所得各阶自相关系数。
1
|
|
|
图 1 和图 2 显示， | ρ 不仅随着 | φ 的增大而增大，也随着 |θ 增加而增加。而且，序列与相依成
1 1 1
|
|
|
分的相关系数 r 也存在与 | ρ 一致的变化趋势，即随着 | φ 与 |θ 的增大而增大。由此可知，对含有
1 1 1
ARMA（1，1）相依成分的序列而言，相关系数可以刻画其相依变异程度。
0.8 0.05 0.1
0.6 -0.05 0 0.05
0.41
自相关系数 -0.2 0 自相关系数 -0.15 自相关系数 -0.05 0
0.2
-0.1
-0.4 -0.2 -0.1
-0.6 -0.25 -0.15
-0.8 -0.3 -0.2
0 5 10 15 20 0 5 10 15 20 0 5 10 15 20
阶数 阶数 阶数
（a）φ = -0.9，θ = 0.2，r = 0.9109 （b）φ = -0.5，θ = 0.2，r = 0.5489 （c）φ = -0.2，θ = 0.2，r = 0.2684
1 1 1 1 1 1
图 1 滑动平均系数 θ 固定时的各阶自相关系数
1
0.1 0.1 0.1
0.05 0
0
自相关系数 -0.05 自相关系数 -0.1 自相关系数 -0.1
0
-0.2
-0.2
-0.1
-0.3
-0.15 -0.3 -0.4
-0.2 -0.4 -0.5
0 5 10 15 20 0 5 10 15 20 0 5 10 15 20
阶数 阶数 阶数
（a）φ = 0.2，θ = 0.2，r = 0.2912 （b）φ = 0.2，θ = 0.5，r = 0.4438 （c）φ = 0.2，θ = 0.9，r = 0.6851
1 1 1 1 1 1
图 2 自回归系数 φ 固定时的各阶自相关系数
1
［7］
3.2.2 ARMA（1，2）模型 自相关系数可以描述水文序列的相依程度 ，在 ARMA（1，2）模型中，式
2
（27）显示 r 与参数 φ 、θ 、θ 有关，而滑动平均系数和自回归系数的参数解与样本自相关系数存在
1 1 2
函数关系，所以 r 与自相关系数具有函数关系。根据式（28）以及自相关系数、自回归系数和滑动平
均系数的关系，选取多组符合条件的 ρ 、 ρ 的值，并由矩估计法 ［26］ 得到 ARMA（1，2）模型的参数
1 2
φ 、 θ 、 θ 值；纯随机成分的生成同 3.2.1 节。ARMA（1，2）序列减去纯随机成分得到相依成分序
1 1 2
列。求出每种 ρ 和 ρ 值下的相关系数，结果如表 4 所示。能够看出：一阶自回归系数 φ 的大小与 ρ
1 2 1 1
的值无关 ［26，28］ ，且当二阶自相关系数 ρ 固定不变时，相关系数 r 随着一阶自相关系数 ρ 的增加而增
2 1
|
|
加；反之，当 ρ 固定时，相关系数 r 随着 ρ 的增加而减小。说明 r 与 | ρ 呈正相关关系、与 | ρ 呈
1 2 1 2
负相关关系，故对于含有 ARMA（1，2）相依成分的序列，其相依性强弱也能用相关系数进行描述。
3.3 模拟序列分析验证 将所提分级方法应用于具有相依成分的模拟序列进行验证。首先从常用的
表 4 不同 ρ 、 ρ 下序列的相关系数
1 2
分组 ρ 1 ρ 2 φ 1 θ 1 θ 2 r
1 -0.1 0.5 0.8000 0.0205 -0.0086 0.7529
ρ 固定 2 0.3 0.5 0.8000 0.0105 -0.0038 0.7663
2
3 0.7 0.5 0.8000 0.0008 0.0009 0.7748
1 0.5 -0.2 -0.5000 0.0230 0.0011 0.5230
ρ 固定 2 0.5 0.4 0.2500 -0.0089 -0.0133 0.2781
1
3 0.5 0.8 0.1250 -0.0314 -0.0756 0.1406
— 799 —