Page 44 - 2021年第52卷第7期

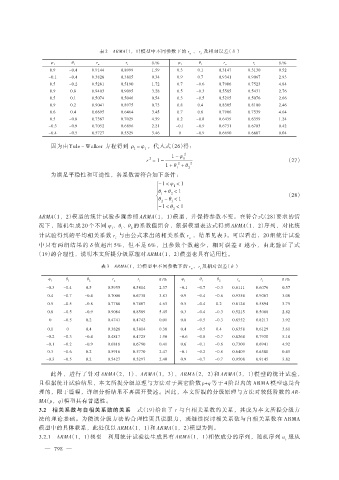
表 2 ARMA（1，1）模型中不同参数下的 r 、 r 及相对误差（ δ ）
i
a
φ θ r r φ θ r r
1 1 a i δ /% 1 1 a i δ /%
0.9 -0.4 0.9144 0.8999 1.59 0.3 0.1 0.3147 0.3130 0.52
-0.1 -0.4 0.3828 0.3815 0.34 0.9 0.7 0.9341 0.9067 2.93
0.5 -0.2 0.5281 0.5190 1.72 0.7 -0.6 0.7906 0.7523 4.84
0.9 0.8 0.9403 0.9095 3.28 0.5 -0.3 0.5585 0.5431 2.76
0.5 0.1 0.5074 0.5046 0.54 0.3 -0.5 0.5215 0.5076 2.66
0.9 0.2 0.9041 0.8975 0.73 0.8 0.4 0.8305 0.8100 2.46
0.6 0.4 0.6695 0.6464 3.45 0.7 0.6 0.7906 0.7539 4.64
0.5 -0.8 0.7367 0.7029 4.59 0.2 -0.8 0.6439 0.6359 1.24
-0.3 -0.9 0.7052 0.6896 2.21 -0.1 -0.9 0.6731 0.6703 0.42
-0.4 -0.5 0.5727 0.5529 3.46 0 -0.9 0.6690 0.6687 0.04
因为由Yule - Walker 方程得到 ρ = φ ，代入式（26）得：
1 1
1 - φ 2
r = 1 - 1 （27）
2
1 + θ + θ 2
2
1 2
为满足平稳性和可逆性，各系数需符合如下条件：
ì-1 < φ < 1
ï
1
ïθ + θ < 1
í 1 2 （28）
ï θ - θ < 1
ï 2
1
î -1 < θ < 1
2
ARMA（1，2）模型的统计试验步骤参照 ARMA（1，1）模型，并保持参数不变。在符合式（28）要求的情
况下，随机生成 20 个不同 φ 、θ 、θ 的系数值组合，依据模型表达式得到 ARMA（1，2）序列，对比统
1 1 2
计试验得到的平均相关系数 r 与由公式求出的相关系数 r ，结果见表 3。可以看出，20 组统计试验
i
a
中只有两组结果的 δ 值超出 5%，但不足 6%，且参数个数越少，相对误差 δ 越小，由此验证了式
（19）的合理性，说明本文所提分级原理对 ARMA（1，2）模型也具有适用性。
表 3 ARMA（1，2）模型中不同参数下的 r 、r 及相对误差（ δ ）
i
a
φ θ θ r r δ /% φ θ θ r r δ /%
1 1 2 a i 1 1 2 a i
-0.3 -0.4 0.5 0.5955 0.5814 2.37 -0.1 -0.7 -0.3 0.6111 0.6076 0.57
0.4 -0.7 -0.4 0.7006 0.6738 3.83 0.9 -0.4 -0.6 0.9354 0.9067 3.06
0.5 -0.5 -0.8 0.7766 0.7407 4.63 0.5 -0.4 0.2 0.6124 0.5894 3.75
0.8 -0.5 -0.9 0.9084 0.8589 5.45 0.3 -0.4 -0.3 0.5215 0.5068 2.82
0 -0.5 0.2 0.4741 0.4742 0.01 0.8 -0.5 -0.3 0.8552 0.8217 3.92
0.1 0 0.4 0.3828 0.3814 0.38 0.4 -0.5 0.4 0.6358 0.6129 3.61
-0.2 -0.3 -0.4 0.4817 0.4725 1.90 -0.6 -0.8 -0.7 0.8364 0.7930 5.18
-0.1 -0.2 -0.9 0.6818 0.6790 0.41 0.6 -0.1 -0.6 0.7300 0.6941 4.92
0.3 -0.6 0.2 0.5916 0.5770 2.47 -0.1 -0.2 -0.8 0.6409 0.6380 0.45
-0.3 -0.5 0.2 0.5427 0.5297 2.40 0.9 -0.7 -0.7 0.9508 0.9145 3.82

此外，进行了针对 ARMA（2，1）、ARMA（1，3）、ARMA（2，2）和 ARMA（3，1）模型的统计试验，
且根据统计试验结果，本文所提分级原理与方法对于其它阶数 p+q 等于 4 阶以内的 ARMA 模型也是合
理的，限于篇幅，详细分析结果不再展开赘述。因此，本文所提的分级原理与方法对较低阶数的 AR⁃
MA（p，q）模型具有普适性。
3.2 相关系数与自相关系数的关系 式（19）给出了 r 与自相关系数的关系，其成为本文所提分级方

法的理论基础。为使该分级方法的合理性更具说服力，现继续探讨相关系数与自相关系数在 ARMA
模型中的具体联系，此处仅以 ARMA（1，1）和 ARMA（1，2）模型为例。

3.2.1 ARMA（1，1）模型 利用统计试验法生成具有 ARMA（1，1）相依成分的序列，随机序列 u 服从
t
— 798 —