Page 21 - 2022年第53卷第5期

河中游河道特性及整治研究》，对淮河的河性进行了较为系统的总结，揭示了淮河的水沙输移特性，
剖析了河湖演变机理，预估了淮河床面形态的变化趋势，为进一步科学治淮奠定理论基石。

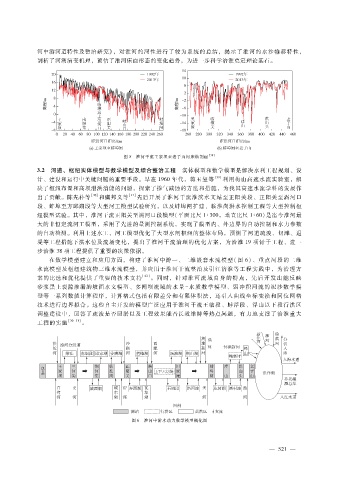
图 ５ 淮河干流王家坝至老子山河床纵剖面 ［３８］

３．２ 河道、枢纽实体模型与数学模型及综合整治工程 实体模型和数学模型是解决水利工程规划、设
计、建设和运行中关键问题的重要手段。早在 １９６０年代，蒋玉玺等 ［３９］ 利用梅山高速水流实验室，解
决了枢纽布置和高坝泄洪消能的问题，探索了掺气减蚀的方法和措施，为我国高速水流学科的发展作
出了贡献。陈先朴等 ［４０］ 和虞邦义等 ［４１］ 先后开展了淮河干流淮滨水文站至正阳关段、正阳关至涡河口
段、蚌埠至方邱湖段等大型河工模型试验研究，以及蚌埠闸扩建、临淮岗洪水控制工程等大型控制枢
纽模型试验。其中，淮河干流正阳关至涡河口段模型（平面比尺 １∶３００，垂直比尺 １∶６０）是迄今淮河最
大的非恒定流河工模型，采用了先进的量测控制系统，实现了模型内、外边界的自动控制和水力参数
的自动检测。利用上述水工、河工模型优化了大型水闸枢纽的整体布局，预测了河道疏浚、切滩、退
堤等工程措施下洪水位及流场变化，提出了淮河干流治理的优化方案，为治淮 １９项骨干工程、进一
步治淮 ３８项工程提供了重要的决策依据。
在数学模型建立和应用方面，构建了淮河中游一、二维嵌套水流模型（图 ６）、重点河段的二维
水流模型及枢纽建筑物三维水流模型，并应用于淮河干流整治及引江济淮等工程实践中，为治理方
案的比选和优化提供了重要的技术支持 ［４２］ 。同时，针对淮 河流 域自 身 的 特点，先 后 开 发出能反映
砂浆黑土裂隙渗漏的坡面水文模型、多闸坝流域的水量 － 水质数学模型、弱冲积河流的泥沙数学模
型等一系列数值计算程序，计算格式包括有限差分和有限体积法，还引入曲线坐标变换和同位网格
技术进行边界拟合。这些自主开发的模型广泛应用于淮河干流王临段、蚌浮段、浮山以下段行洪区
调整建设中，回答了疏浚是否回淤以及工程效果能否长效维持等热点问题，有力地支撑了治淮重大
工程的实施 ［３０ － ３１］ 。

图 ６ 淮河中游水动力数学模型概化图

— ５ ２ １ —