Page 41 - 2022年第53卷第5期

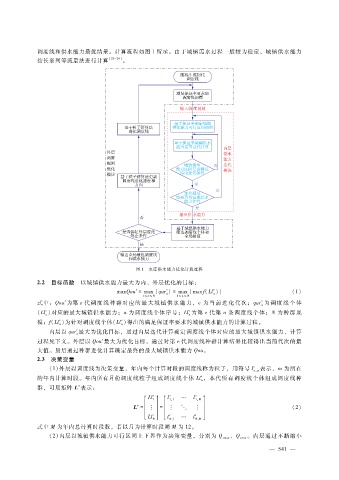
调度线和供水能力最优结果。计算流程如图 １所示。由于城镇需水过程一般较为稳定，城镇供水能力
按长系列等流量法进行计算 ［２３ － ２４］ 。

图 １ 水库供水能力优化计算流程
２．２ 目标函数 以城镇供水能力最大为内、外层优化的目标：
ｅ
ｅ
ｅ
ｍａｘＱｏｕ＝ｍａｘ｛ｑｕｒ｝ ＝ｍａｘ｛ｍａｘｆ（Ｌｌ）｝ （１）
ｎ
ｎ
１ ≤ｎ ≤Ｎ １ ≤ｎ ≤Ｎ
ｅ
ｅ
式中：Ｑｏｕ为第 ｅ代 调 度线种 群对 应的 最 大城镇 供水 能 力，ｅ为 当 前 进 化 代 次；ｑｕｒ为 调 度 线 个 体
ｎ
ｅ
ｅ
（ Ｌｌ）对应的最大城镇供水能力；ｎ为调度线个体序号；Ｌｌ为第 ｅ代第 ｎ条调度线个体；Ｎ为种群规
ｎ
ｎ
ｅ
ｅ
模；ｆ（Ｌｌ）为针对调度线个体（Ｌｌ）得出的满足保证率要求的城镇供水能力的计算过程。
ｎ
ｎ
ｅ
内层以 ｑｕｒ最大为优化目标，通过内层迭代计算确定调度线个体对应的最大城镇供水能力，计算
ｎ
ｅ
过程见下文。外层以 Ｑｏｕ最大为优化目标，通过对第 ｅ代调度线种群计算结果比较得出当前代次的最
大值。最后通过种群进化计算确定最终的最大城镇供水能力 Ｑｏｕ。
２．３ 决策变量
ｅ
（１）外层以调度线为决策变量，年内每个计算时段的调度线称为粒子，用符号 ｌ 表示，ｍ为所在
ｎ ，ｍ
ｅ
的年内计算时段。年内所有月份调度线粒子组成调度线个体 Ｌｌ，本代所有调度线个体组成调度线种
ｎ
ｅ
群，可用矩阵 Ｌ表示：
ｅ
ｅ
ｅ
Ｌｌ ｌ … ｌ
１，Ｍ
１，１
１
ｅ
Ｌ ＝  ＝    （２）
ｅ
ｅ
ｅ
Ｌｌ ｌ … ｌ
Ｎ
Ｎ ，Ｍ
Ｎ ，１
式中 Ｍ为年内总计算时段数，若以月为计算时段则 Ｍ为 １２。
（ ２）内层以城镇供水能力可行区间上下界作为决策变量，分别为 Ｑ 、Ｑ 。内层通过不断缩小
ｓｍａｘ ｓｍｉｎ
— ５ ４ １ —