Page 91 - 2022年第53卷第5期

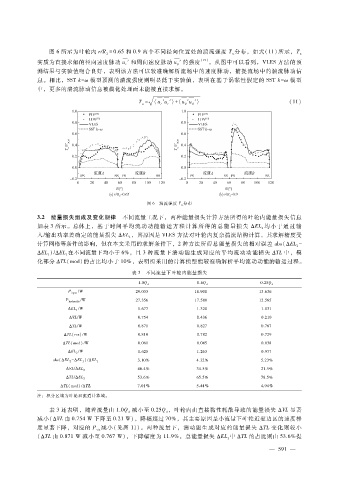
图 ６所示为叶轮内 ｒ?Ｒ ＝ ０．６５和 ０．９两个不同径向位置处的湍流强度 Ｔ分布，如式（１１）所示，Ｔ
２ ｕ ｕ
实质为直接求解的径向速度脉动 ｕ′和周向速度脉动 ｕ′的强度 ［１５］ 。从图中可以看到，ＶＬＥＳ方法的预
ｒ
θ
测结果与实验值吻合良好，表明该方法可以较准确解析流场中的速度脉动，捕捉流场中的湍流脉动信
息。相比，ＳＳＴｋ － ω模型预测的湍流强度则明显低于实验值，表明在基于涡黏性假定的 ＳＳＴｋ － ω模型
中，更多的湍流脉动信息被模化处理而未能被直接求解。

槡
Ｔ ＝ 〈ｕ′ｕ′〉 ＋ 〈ｕ′ｕ′〉 （１１）
ｕ ｒ ｒ θ θ

图 ６ 湍流强度 Ｔ ｕ 分布

３．２ 能量损失组成及变化规律 不同流量工况下，两种能量损失计算方法所得的叶轮内能量损失信息
如表 ３所示。总体上，基于时间平均流动动能输运 方程 计算 所得 的总 能 量 损失 Δ ＥＬ均小 于 通过输
２
入?输出功率差确定的能量损失 Δ ＥＬ，其原因是 ＶＬＥＳ方法对叶轮内复杂湍流结构计算，其求解精度受
１
计算网格等条件的影响，但在本文采用的求解条件下，２种方法所得总能量损失的相对误差 ａｂｓ（ Δ ＥＬ－
２
Δ ＥＬ）? Δ ＥＬ在不同流量下均小于 ６％，且 ３种流量下湍动能生成对应的平均流动动能损失 Δ ＴＬ中，模
１
１
化部分 Δ ＴＬ（ｍｏｄ）的占比均小于 １０％，表明所采用的计算模型能较准确解析平均流动动能的输运过程。
表 ３ 不同流量下叶轮内能量损失

１．０Ｑ ｄ ０．６Ｑ ｄ ０．２５Ｑ ｄ
Ｐ ｉｎｐｕｔ ?Ｗ ２９．０３３ １８．９００ １３．６３６
Ｐ ｈｙｄｒａｕｌｉｃ ?Ｗ ２７．３５６ １７．５８０ １２．５６５
Δ ＥＬ １ ?Ｗ １．６７７ １．３２０ １．０３１
Δ ＶＬ?Ｗ ０．７５４ ０．４３６ ０．２１０
Δ ＴＬ?Ｗ ０．８７１ ０．８２７ ０．７６７
Δ ＴＬ（ｒｅｓ）?Ｗ ０．８１０ ０．７８２ ０．７２９
Δ ＴＬ（ｍｏｄ）?Ｗ ０．０６１ ０．０４５ ０．０３８
Δ ＥＬ ２ ?Ｗ １．６２５ １．２６３ ０．９７７
－
ａｂｓ （ Δ ＥＬ ２ Δ ＥＬ １ ）? Δ ＥＬ １ ３．１０％ ４．３２％ ５．２３％
４６．４％ ３４．５％ ２１．５％
Δ ＶＬ? Δ ＥＬ ２
５３．６％ ６５．５％ ７８．５％
Δ ＴＬ? Δ ＥＬ ２
Δ ＴＬ（ｍｏｄ）? Δ ＴＬ ７．０１％ ５．４４％ ４．９４％
注：积分区域为叶轮双流道计算域。

表 ３还表明，随着流量由 １．０Ｑ 减小至 ０．２５Ｑ，叶轮内由直接黏性耗散导致的能量损失 Δ ＶＬ显著
ｄ ｄ
减小（ Δ ＶＬ由 ０．７５４Ｗ 下降至 ０．２１Ｗ），降幅超过 ７０％，其主要原因是小流量下叶轮近壁边区的速度梯
度显著下降，对应的 Ｐ 减小（见图 １１）。两种流量下，湍动能生成对应的能量损失 Δ ＴＬ变化则较小
ｖｉｓ
（ Δ ＴＬ由 ０．８７１Ｗ 减小至 ０．７６７Ｗ），下降幅度为 １１．９％，总能量损失 Δ ＥＬ中 Δ ＴＬ的占比则由 ５３．６％提
２
— ５ ９ １ —