Page 90 - 2022年第53卷第5期

２ ∫
Δ ＥＬ ＝ Ｐ ｄＶ ＋ Ｐ ｋ － ｄＶ ＋ Ｐ ｋ － ｄＶ （１０）
∫ ｍｏｄ
∫ ｒｅｓ
ｖｉｓ
Δ ＶＬ Δ ＴＬ（ｒｅｓ） Δ ＴＬ（ｍｏｄ）
式中：Δ ＶＬ为直接黏性损失；Δ ＴＬ（ｒｅｓ）、Δ ＴＬ（ｍｏｄ）分别为与湍动能生成对应的平均流动动能损失的
直接求解部分和模化部分。

３ 结果与讨论

３．１ 网格无关性分析与计算模型验证 选取 ０．２５Ｑ 工况，采用 ５套不同的网格对叶轮内的非定常流
ｄ
动进行模拟，通过与文献［１５］中实验结果的对比，进行 ＶＬＥＳ模型在离心叶轮内流场计算的网格无关
性分析及计算模型准确性验证。
图 ３为不同数量网格计算所得的总能量损失。由图 ３可知，随着网格数量的增加，Ｍ１和 Ｍ２两种
不同损失计算方法所得的叶轮内的能量损失 Δ ＥＬ和 Δ ＥＬ，均随网格数量的增加呈下降趋势，当计算
１ ２
域网格总数大于 ３．４６Ｍ 时（Ｍｅｓｈ３），Δ ＥＬ和 Δ ＥＬ均趋于固定值，且两者之间的相对误差 ａｂｓ（ Δ ＥＬ－
１ ２ ２
Δ ＥＬ）? Δ ＥＬ保持在 ６％以下。图 ４所示的不同网格计算所得的 Δ ＴＬ（ｒｅｓ）与 Δ ＴＬ（ｍｏｄ）表明，随网格数量
１
１
增加，Δ ＴＬ（ｒｅｓ）逐渐增加而 Δ ＴＬ（ｍｏｄ）逐渐减小，在 Ｍｅｓｈ４和 Ｍｅｓｈ５中，Δ ＴＬ（ｍｏｄ）? Δ ＴＬ均小于 １０％，
表明单位时间内生成湍动能所对应的平均流动动能损失 Δ ＴＬ，直接求解部分的占比超过 ９０％，验证了计
算模型的网格收敛性和可靠性，后续以 Ｍｅｓｈ５的计算结果进一步分析叶轮内流动结构和能量损失特性。

图 ３ 能量损失及相对误差 图 ４ Δ ＴＬ（ｒｅｓ）与 Δ ＴＬ（ｍｏｄ）占比

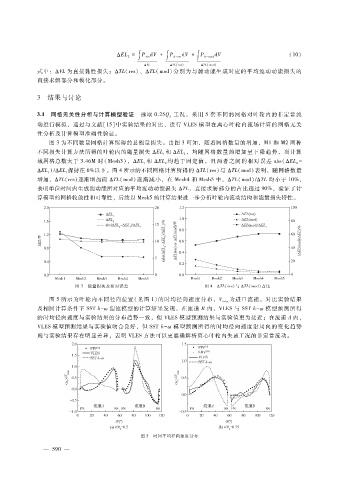
图 ５所示为叶轮内不同径向位置（见图 １）的时均径向速度分布，Ｖ 为进口流速。对比实验结果
ｉｎｌｅｔ
及相同计算条件下 ＳＳＴｋ － ω湍流模型的计算结果发现，在流道 Ｂ内，ＶＬＥＳ与 ＳＳＴｋ － ω模型预测所得
的时均径向速度与实验结果的分布趋势一致，但 ＶＬＥＳ模型预测结果与实验值更为接近；在流道 Ａ内，
ＶＬＥＳ模型预测结果与实验值吻合良好，但 ＳＳＴｋ － ω模型预测所得的时均径向速度沿周向的变化趋势
则与实验结果存在明显差异，表明 ＶＬＥＳ方法可以更准确解析离心叶轮内失速工况的非定常流动。

图 ５ 时间平均径向速度分布

０
— ５ ９ —