Page 114 - 2023年第54卷第3期

汇水单元的产汇流、污染物累积冲刷、管网水动力水质等多个复杂过程进行连续模拟。为定量评价模
拟结果的合理性，选取平均相对误差（ Ｍｅａｎｒｅｌａｔｉｖｅｅｒｒｏｒ，ＭＲＥ）和纳什效率系数（Ｎａｓｈ － ｓｕｔｃｌｉｆｆｅｃｏｅｆｆｉ
ｃｉｅｎｔｏｆｅｆｆｉｃｉｅｎｃｅ ，ＮＳＥ）作为评价指标：
ｓｉｍ
１ ｎ Ｙ － Ｙ ｏｂｓ
ｉ
ｉ
ＭＲＥ ＝ ∑ × １００ ％ （１６）
ｎ ｉ ＝１ Ｙ ｏｂｓ
ｉ
ｎ
ｓｉｍ
ｏｂｓ
∑ （Ｙ － Ｙ ） ２
ｉ
ｉ
ｉ ＝１
ＮＳＥ ＝ １ － （１７）
ｎ
ｏｂｓ
∑ （Ｙ － Ｙ ｍｅａｎ ２
）
ｉ
ｉ ＝１
ｏｂｓ
ｓｉｍ
式中：Ｙ 为第 ｉ个实测值；Ｙ 为第 ｉ个模拟值；Ｙ ｍｅａｎ 为实测平均值；ｎ为实测值个数。
ｉ ｉ
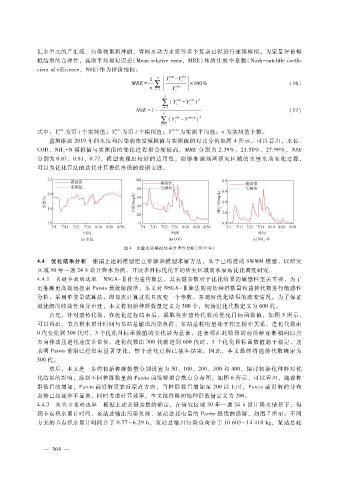
监测断面 ２０１９年的水位和污染物浓度模拟值与实测值的对比分析如图 ４所示，可以看出，水位、
ＣＯＤ、ＮＨ － Ｎ模拟值与实测值的变化过程拟合度较高。ＭＲＥ分别为 ２．３９％、２１．５０％、２７．９９％，ＮＳＥ
３
分别为 ０．８７、０．８１、０．７７，模型表现出较好的适用性，能够准确刻画研究区域的水量水质变化过程，
可以为优化算法的迭代计算提供准确的数据支撑。

图 ４ 水量水质模拟结果合理性分析（２０１９年）

４．４ 优化结果分析 根据上述的模型建立步骤和模型求解方法，基于已构建的 ＳＷＭＭ 模型，以研究
区域 ５０年一遇 ２４ｈ设计降水为例，开展多目标优化下的研究区域雨水泵站优化调度研究。
４．４．１ 关键参数的选取 ＮＳＧＡ － Ⅱ作为遗传算法，其关键参数对于优化结果的敏感性至关重要，为了
更准确更高效地搜索 Ｐａｒｅｔｏ最优解前沿，本文对 ＮＳＧＡ － Ⅱ算法的初始种群数量和遗传代数进行敏感性
分析，采用单变量试算法，即每次计算过程只改变一个参数，并观察优化结果的改变情况。为了保证
最优解的收敛性和分布性，本文将初始种群数量定义为 ３００个，初始进化代数定义为 ６００代。
首先，针对遗传代数，在优化过程结束后，提取每步遗传代数的优化目标函数值，如图 ５所示，
可以看出，节点积水累计时间与泵站总输出污染负荷、泵站总耗电量处于相互博弈关系。进化代数由
０代变化到 ３００代时，３个优化目标函数值的变化最为显著，这表明在此阶段的前沿解逐渐朝向原点
方向移动且进化速度非常快。进化代数由 ３００代前进到 ６００代时，３个优化目标函数值趋于稳定，这
表明 Ｐａｒｅｔｏ前沿已经没有显著变化，整个进化过程已基本结束。因此，本文最终将遗传代数确定为
３００代。
然后，本文进一步将初始种群数量分别设置为 ５０、１００、２００、３００和 ４００，探讨初始化种群对优
化结果的影响，绘制不同种群数量的 Ｐａｒｅｔｏ前沿解拟合散点分布图，如图 ６所示，可以看出，随着种
群数目的增加，Ｐａｒｅｔｏ前沿解更靠近原点方向，当种群数目增加至 ２００以上时，Ｐａｒｅｔｏ前沿解的分布
态势已经逐步不显著，同时考虑计算效率，本文最终将初始种群数量定义为 ２００。
４．４．２ 优化方案的选取 根据上述关键参数的确定，在研究区域 ５０年一遇 ２４ｈ设计降水情景下，得
到节点积水累计时间、泵站总输出污染负荷、泵站总耗电量的 Ｐａｒｅｔｏ最优前沿解，如图 ７所示。不同
方案的节点积水累计时间介于 ０．７７～６．２９ｈ，泵站总输出污染负荷介于 １０６０３～１４４１０ｋｇ，泵站总耗

４
— ３ ６ —