Page 21 - 2023年第54卷第8期

４ 算例分析

采用图 １中含调压室的水电站输水发电系统，其中：
３
Ｚ ＝ １００．０ｍ ，Ｚ ＝ ０．０ｍ ，Ｑ ＝ Ｑ ＝ Ｑ ＝ Ｑ ＝ ４０．０ｍ ?ｓ，Ｌ＝ ２０００．０ｍ ，Ｌ＝ Ｌ＝ ２００．０ｍ ，ｆ＝ ｆ＝
Ｕ Ｄ １０ ２０ ３０ ０ １ ２ ３ １ ２
２
２
ｆ ＝ １０．０ｍ ，ｈ ＝ ２．０ｍ ，α ＝ ０．１２５ｓ?ｍ，ｈ ＝ ０．５ｍ ，ｈ ＝ ０．５ｍ ，ｃ＝ ｃ＝ ｃ＝ １０００．０ｍ?ｓ ，调压室面
３
ｗｍ０
ｗ０
３
２
ｗｄ０
１
２
积 Ｆ ＝ ２．３３ × Ｆ ＝ ２．３３ × （２０００．０ × １０．０）?［２．０ × ０．１２５ × ９．８ × （１００．０ － ２．０ － ３ × ０．５ － ３ × ０．５）］ ≈２００．０ｍ 。
ｔｈ
分别采用文中的二阶刚性水体模型、三阶刚性水体模型、弹性模型来验证系统小波动稳定性。其
中弹性模型为式（２７）（２８）联合构建的偏微分方程组，通过特征线法数值求解；二阶刚性水体模型与三
阶刚性水体模型均为常微分方程组，为了充分考虑实际系统中非线性项的影响，不采用式（ １２）、式
（ １８）建立的线性化模型，而是直接通过式（１）至式（１０）建立非线性模型，采用四阶龙格—库塔法进行
数值求解。其中，二阶刚性系统的动力模型为：
ｄＺ Ｔ Ｑ － Ｑ ２
１
＝
ｄｔ Ｆ
ｄＱ ｇｆ （ ５１）
１ １
＝ （Ｚ － Ｚ － ｈ）
ｄｔ Ｌ Ｕ Ｔ ｗ
１
Ｑ（Ｚ － Ｚ － ｈ － ｈ ） ＝Ｑ（Ｈ － Ｈ ）
Ｄ
ｗｄ
ｗｍ
Ｄ０
Ｕ０
０
２
Ｔ
三阶刚性系统的动力模型为：
ｄＺ Ｔ Ｑ － Ｑ ２
１
＝
ｄｔ Ｆ
ｄＱ ｇｆ
１ １
＝ （Ｚ － Ｚ － ｈ） （ ５２）
ｄｔ Ｌ Ｕ Ｔ ｗ
１
ｄＱ ２ ｇｆｆ Ｑ（Ｈ － Ｈ ）
Ｄ０
２ ３
Ｕ０
０
＝ ［Ｚ － Ｚ － ｈ － ｈ － ］
ｄｔ Ｌｆ ＋ Ｌｆ Ｔ Ｄ ｗｍ ｗｄ Ｑ ２
２ ３
３ ２
三种模型的系统扰动均为上游水库的水位变化，
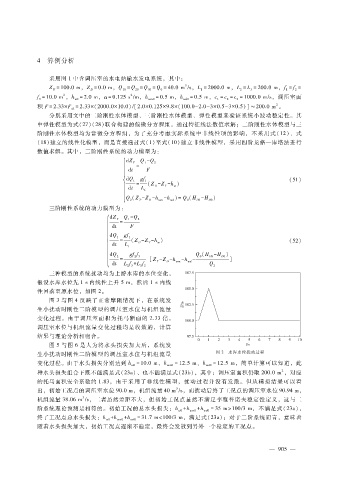
假设水库水位先 １ｓ内线性上升 ５ｍ，然后 １ｓ内线
性回落至原水位，如图 ２。
图 ３与图 ４反映了正常摩阻情况下，在系统发
生小扰动时刚性二阶模型的调压室水位与机组流量
变化过程。由于调压室面积为托马断面的 ２．３３倍，
调压室水位与机组流量变化过程均是收敛的，计算
结果与理论分析相吻合。
图 ５与图 ６是人为将水头损失加大后，系统发
生小扰动时刚性二阶模型的调压室水位与机组流量 图 ２ 水库水位扰动过程
变化过程。由于水头损失分别达到 ｈ ＝ １０．０ｍ 、ｈ ＝ １２．５ｍ 、ｈ ＝ １２．５ｍ ，简单计算可以知道，此
ｗ０ ｗｍ０ ｗｄ０
２
种水头损失组合下既不能满足式（ ２３ａ）、也不能满足式（２３ｂ），其中：调压室面积仍取 ２００．０ｍ ，对应
的托马面积安全系数约 １．８３，由于采用了非线性模型，扰动过程并没有发散。但从模拟结果可以看
３
出，初始工况点的调压室水位 ９０．０ｍ，机组流量 ４０ｍ ?ｓ，而扰动后终了工况点的调压室水位 ９０．９４ｍ，
３
机组流量 ３８．０６ｍ ?ｓ，二者虽然差距不大，但初始工况点显然不满足李雅普诺夫稳定性定义，这与二
阶系统理论预测是相符的。初始工况的总水头损失：ｈ ＋ ｈ ＋ ｈ ＝ ３５ｍ＞１００?３ｍ ，不满足式（２３ａ），
ｗ０ ｗｍ０ ｗｄ０
终了工况点总水头损失：ｈ ＋ ｈ ＋ ｈ ＝ ３１．７ｍ＜１００?３ｍ ，满足式（２３ａ）；对于二阶系统而言，意味着
ｗ０
ｗｍ０
ｗｄ０
随着水头损失加大，初始工况点逐渐不稳定，最终会发散到另外一个稳定的工况点。
— ９ ０ ５ —