Page 22 - 2023年第54卷第8期

２
２
图 ３ 调压室水位变化过程（刚性二阶模型）（Ｆ ＝ ２００ｍ ） 图 ４ 机组流量变化过程（刚性二阶模型）（Ｆ ＝ ２００ｍ ）
＝
＝
＝
＝
ｈ ｗ０ ２．０ｍ 、ｈ ｗｍ０ ０．５ｍ 、ｈ ｗｄ０ ０．５ｍ ｈ ｗ０ ２．０ｍ 、ｈ ｗｍ０ ０．５ｍ 、ｈ ｗｄ０ ０．５ｍ
＝
＝

２
２
图 ５ 调压室水位变化过程（刚性二阶模型）（Ｆ ＝ ２００ｍ ） 图 ６ 机组流量变化过程（刚性二阶模型）（Ｆ ＝ ２００ｍ ）
＝
＝
＝
＝
＝
ｈ ｗ０ １０．０ｍ 、ｈ ｗｍ０ １２．５ｍ 、ｈ ｗｄ０ １２．５ｍ ｈ ｗ０ １０．０ｍ 、ｈ ｗｍ０ １２．５ｍ 、ｈ ｗｄ０ １２．５ｍ
＝
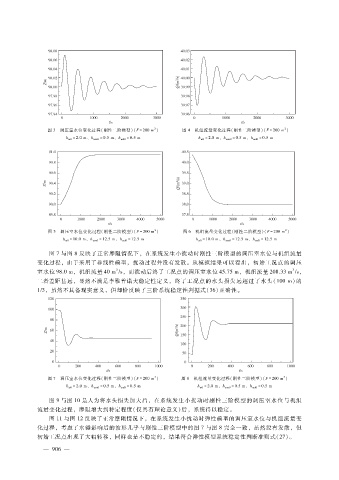
图 ７与图 ８反映了正常摩阻情况下，在系统发生小扰动时刚性三阶模型的调压室水位与机组流量
变化过程，由于采用了非线性模型，扰动过程并没有发散。从模拟结果可以看出，初始工况点的调压
３
３
室水位 ９８．０ｍ，机组流量 ４０ｍ ?ｓ，而扰动后终了工况点的调压室水位 ４５．７５ｍ，机组流量 ２０８．３３ｍ ?ｓ，
二者差距甚远，显然不满足李雅普诺夫稳定性定义，终了工况点的水头损失远超过了水头（ １００ｍ）的
１?３，虽然不具备现实意义，但却恰反映了三阶系统稳定性判据式（３６）正确性。

２
２
图 ７ 调压室水位变化过程（刚性三阶模型）（Ｆ ＝ ２００ｍ ） 图 ８ 机组流量变化过程（刚性三阶模型）（Ｆ ＝ ２００ｍ ）
＝
＝
＝
＝
＝
＝
ｈ ｗ０ ２．０ｍ、ｈ ｗｍ０ ０．５ｍ、ｈ ｗｄ０ ０．５ｍ ｈ ｗ０ ２．０ｍ、ｈ ｗｍ０ ０．５ｍ、ｈ ｗｄ０ ０．５ｍ
图 ９与图 １０是人为将水头损失加大后，在系统发生小扰动时刚性三阶模型的调压室水位与机组
流量变化过程，摩阻增大到特定程度（仅具有理论意义）后，系统得以稳定。
图 １１与图 １２反映了正常摩阻情况下，在系统发生小扰动时弹性模型的调压室水位与机组流量变
化过程，考虑了水锤影响后的波形几乎与刚性三阶模型中的图 ７与图 ８完全一致，虽然没有发散，但
初始工况点出现了大幅转移，同样也是不稳定的，结果符合弹性模型系统稳定性判断准则式（２７）。
６
— ９ ０ —