Page 41 - 2023年第54卷第8期

式中 Ｖ 和 Ｖ 分别为粗料密堆积体中孔隙与固相的体积。作为对比，不剔除细料的堆石料（试样Ⅱ）也
ａ１ ｓ１
进行了最大干密度试验。试样Ⅱ相比于试样Ⅰ，增加的细料含量造成的影响包含两个方面：一是对孔
隙体积的影响，另一个是对固相体积的影响。试样Ⅱ的孔隙比写作
Ｖ ＋ Ｖ
ｅ ＝ ａ１ ａ２ （９）
ｍｉｎ
Ｖ ＋ Ｖ
ｓ１ ｓ２
式中 Ｖ 和 Ｖ 分别为试样Ⅱ相较于试样Ⅰ，增加细料造成的孔隙和固相的体积增量。
ａ２ ｓ２
固相部分的体积 Ｖ 和 Ｖ 是固定不变的，可以根据级配曲线中截断粒径对应的百分比得知；对于
ｓ１ ｓ２
孔隙部分的体积，Ｖ 可以根据本文提出的堆积算法得到，而 Ｖ 的值并不固定，由于堆积的模式不同，
ａ１ ａ２
当细料填充粗料的孔隙时，Ｖ 的取值甚至可能为负值。
ａ２
假定增加细料会同时改变孔隙和固相的体积，但不同试样中细料的孔隙与固相的体积比值为一恒
定值，即
Ｖ ?Ｖ ＝ ｅ＝ ｃｏｎｓｔ （１０）
ａ２ ｓ２ ２
该假定的主要依据是试验中的砂砾石料来源于同一料源，且宽级配的堆石料试样中，细料部分的
堆积与粗骨料的堆积独立性较高，因此小于最小筛径的颗粒级配虽然未知，却基本相同。
结合式（８）—（１０），不难建立 ｅ 与粗料最小孔隙比 ｅ′之间的关系
ｍｉｎ
ｍｉｎ
ｅ － ｅ′ ＝ θ ｅ （１１）
ｍｉｎ ｍｉｎ ２
式中 θ 为截断粒径对应的细料含量百分比。
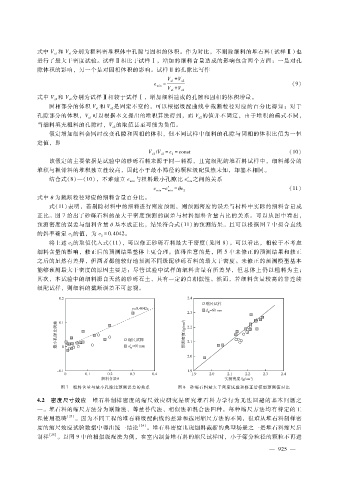
式（ １１）表明，若剔除材料中的细料进行密度预测，则预测密度的误差与材料中实际的细料含量成
正比。图 ７给出了砂砾石料的最大干密度预测的误差与材料细料含量占比的关系。可以从图中看出，
预测密度的误差与细料含量 θ 基本成正比，结果符合式（１１）的预测结果。且可以根据图 ７中拟合直线
的斜率确定 ｅ的值，为 ｅ＝ ０ ．４０４２。
２
２
将上述 ｅ的取值代入式（１１），可以修正砂砾石料最大干密度（见图 ８）。可以看出，相较于不考虑
２
细料含量的影响，修正后的预测结果整体上更合理。值得注意的是，图 ５中未修正的预测结果和修正
之后的虽然有差异，但两者都能较好地预测不同级配砂砾石料的最大干密度。未修正的预测模型基本
能够预测最大干密度的原因主要是：尽管试验中试样的细料含量有所差异，但总体上仍以粗料为主；
其次，本试验中的细料源自天然的砂砾石土，具有一定的自相似性。然而，若细料含量较高的非连续
级配试样，则细料的截断误差不可忽视。

图 ７ 细料含量与最小孔隙比预测误差的关系 图 ８ 砂砾石料最大干密度试验和修正后模型预测值对比

４．２ 密度尺寸效应 堆石料制样密度的缩尺效应研究是研究堆石料力学行为无法回避的基本问题之
一。堆石料的缩尺方法分为剔除法、等量替代法、相似法和混合法四种，每种缩尺方法均有特定的工
程使用范畴 ［２３］ 。因为不同工程的堆石料级配曲线的差异和选用缩尺方法的不同，很难从堆石料制样密
度的缩尺效应试验数据中得出统一结论 ［２４］ 。堆石料密度出现细料截断的典型场景之一是堆石料缩尺后
制样 ［２５］ 。以图 ９中的相似级配法为例，在室内制备堆石料的缩尺试样时，小于筛分粒径的颗粒不再进

— ９ ２ ５ —