Page 17 - 2023年第54卷第11期

［２６］
Ｍｉｃｈｅｌ 认为上游水流绕过冰块时，由于局部的水流加速和分离，引起冰块底面压力减少，浮力
作用减弱，经分析得出的临界下潜条件为：
Ｖ
＝ ２ （４）
槡
( )
ｇｔ １ － ρ ｉ
槡 ρ
式（４）可重组为：
Ｖ ｔ ρ － ρ ｉ
＝ ２ ·
ｇＨ 槡 Ｈ ρ （５）
槡
比较式（ ３）（５），可以看出，对于同样的 ｔ?Ｈ，式（５）算出的临界下潜速度相对要大。对于式（４），
为考虑冰塞体内冰堆积的空隙影响，Ｍｉｃｈｅｌ在计算式中引入了孔隙率 Ｐ：
ｊ
Ｖ
＝ ２ （６）
槡
( )
ｇｔ １ － ρ ｉ ( １ － Ｐ)
槡 ρ
ｊ
并且 Ｍｉｃｈｅｌ得出了类似 Ｐａｒｉｓｅｔ和 Ｈａｕｓｓｅｒ的式（３）：
Ｖ ｔ ρ － ρ ｉ ｔ ( )
ｔ
＝ ２ ·
ｇＨ 槡 Ｈ ρ ( １ － Ｐ) Ｈ １ － Ｈ （７）
ｊ
槡
式（７）比式（４）多了孔隙率 Ｐ的影响，只是 Ｍｉｃｈｅｌ在推导时，孔隙率是指上游冰盘的孔隙率，而推导
ｊ
过程中对于冰盖下的冰塞体采用了相同的孔隙率，显然两者是有区别的。
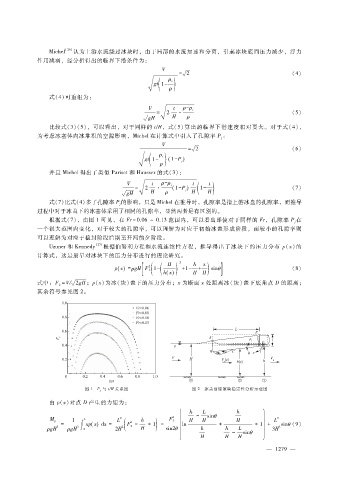
根据式（７），由图 １可见，在 Ｆｒ ＝ ０．０６～０．１３ 范围内，可以看出即使对于同样的 Ｆｒ，孔隙率 Ｐ在
ｊ
一个很大范围内变化，对于较大的孔隙率，可以理解为对应于初始冰盖形成阶段，而较小的孔隙率则
可以理解为对应于稳封阶段后期至开河前夕阶段。
［２７］
Ｕｚｕｎｅｒ和 Ｋｅｎｎｅｄｙ 根据伯努利方程和水流连续性方程，推导得出了冰块下的压力分布 ｐ（ｘ）的
计算式，这是最早对冰块下的压力分布进行的理论研究。
Ｈ
[ ２ ( ( ) ２ ｈ ｘ ) ]
ｐｘ ＝ ρ ｇＨ Ｆ ２ １ － ｈｘ ＋ １ － ＋ ｓｉｎ θ （８）
()
()
Ｈ Ｈ
式中：Ｆ ＝ Ｖ?２ｇＨ；ｐ（ｘ）为冰（块）盖下的压力分布；ｘ为断面 ｘ处距离冰（块）盖下底角点 Ｄ的距离；
槡
２
其余符号参见图 ２。

图 １ Ｐ ｊ 与 ｔ?Ｈ关系图 图 ２ 冰盖前缘冰块稳定性分析示意图

由 ｐ（ｘ）对点 Ｄ产生的力矩为：
ｈ Ｌ ｈ
－ ｓｉｎ θ
２
Ｍ ｐ １ Ｌ Ｌ ２ ｈ Ｆ ２ Ｈ Ｈ Ｈ Ｌ
３
)
２
ｘｐｘ ｄｘ ＝
＝ ３∫ () ２( Ｆ － ＋１ － ｌｎ ＋ ＋１ ＋ ｓｉｎ θ （９）
２
ρ ｇＨ ３ ρ ｇＨ ０ ２Ｈ Ｈ ｓｉｎ２ θ ｈ ｈ Ｌ ３Ｈ ３
－ ｓｉｎ θ
Ｈ Ｈ Ｈ
２
— １ ７ ９ —