Page 21 - 2023年第54卷第11期

Ｖ ｔ ｔ ｌ
(
ｕ ｉ ｉ ｉ
＝ ｆ ， ， ，ｓ ) （２５）
ｉ
槡 ｇｔ Ｈ ｌ ｂ
ｉ
ｉ
ｉ
?。
式中：ｔ、ｌ、ｂ分别是冰块厚度、长度和宽度，其下标 ｉ可以理解为冰块尺寸大小不一；ｓ ＝ ρ ｉ ρ
ｉ
ｉ
ｉ
ｉ
［３６］
［２７］
［２４］
Ｂｅｌｔａｏｓ认为 Ｐａｒｉｓｅｔ和 Ｈａｕｓｓｅｒ 、Ｕｚｕｎｅｒ和 Ｋｅｎｎｅｄｙ 和 Ｃｈｅｅ和 Ｈａｇｇａｇ 的研究结果都是上式
不同形式的具体表达。但也正如 Ｂｅｌｔａｏｓ所说那样，有关式（２５）分析解的表达式至今未见，式（２５）中，
明确出现了 ｌ?ｂ因子，迄今为止，众多研究者的计算式中几乎没有出现该因子。
ｉ
ｉ
隋觉义等 ［３７］ 从 １９８６年至 １９９１年，在黄河河曲段封冻冰盖前缘处进行了天然河道天然真冰的下潜
试验研究，试验冰块加工成长和宽相等的矩形六面体，厚度变化为 ０．０５～０．３１ｍ，大致对应封河前夕
上游来冰的冰厚变化范围，试验中 ｔ?Ｌ分为 ５个档次，分别为 ｔ?Ｌ ＝ ０．１ ，０．２，０．３，０．４，０．５，试验得出了
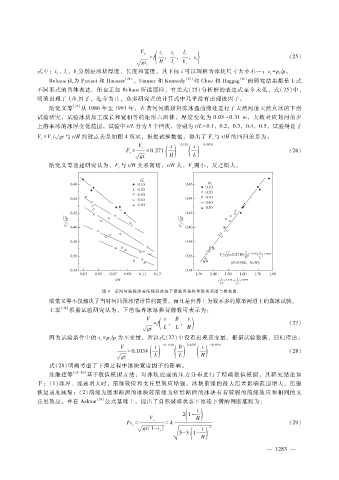
Ｆ ＝ Ｖ? ｇｔ与 ｔ?Ｈ的散点关系如图 ４所示，根据试验数据，得出了 Ｆ与 ｔ?Ｈ的回归关系为：
ｃ 槡
ｃ ｃ
Ｖ ｃ ｔ － ０．１０１ ｔ － ０．０８７８
Ｆ ＝ ＝ ０ ．２７１ ( ) ( ) （２６）
ｃ
槡 ｇｔ Ｈ Ｌ
隋觉义等通过研究认为，Ｆ与 ｔ?Ｈ关系密切，ｔ?Ｈ大，Ｆ则小，反之则大。
ｃ
ｃ

图 ４ 黄河河曲段冰盖前缘处冰块下潜临界条件参数关系图与相关图
隋觉义等不仅解决了当时河曲段冰情计算的需要，而且是世界上为数不多的原型河道上的真冰试验。
王军 ［３８］ 根据试验研究认为，下潜临界冰厚弗劳德数可表示为：
Ｖ ｔ Ｂ ｔ
(
＝ ｆ ， ， ) （２７）
槡 ｇｔ Ｌ Ｌ Ｈ
因为试验条件中的 ｓ ＝ ρ ｉ ρ
?为不变量，所以式（２７）中没有出现该变量。根据试验数据，回归得出：
ｉ
Ｖ ｔ － ０ ．１１２９ Ｂ ０．２５９７ ｔ － ０ ．４９１９
＝ ０ ．１０３４ ( ) ( ) ( ) （２８）
槡 ｇｔ Ｌ Ｌ Ｈ
式（ ２８）明确考虑了下潜过程中冰块宽度因子的影响。
练继建等 ［３９ － ４０］ 基于数值模拟方法，对冰块底面的压力分布进行了精确数值模拟，其研究结论如
下：（ １）冰厚、流速增大时，前缘效应和文丘里效应增强，冰块前缘的最大压差影响范围增大，压强
恢复速度减慢；（２）前缘为圆形断面的冰块较前缘为矩形断面的冰块有着较弱的前缘效应和相同的文
丘里效应。并在 Ａｓｈｔｏｎ ［２８］ 公式基础上，提出了自然破碎状态下冰凌下潜的判断准则为：
( )
２１ － ｔ
Ｖ ｃ Ｈ
Ｆｒ ＝ ＝ｋ （２９）
ｃ
槡 ｇｔ（１ － ｓ） ５ － ３ １ － ｔ ２
( )
ｉ
槡 Ｈ
— １ ８ ３ —
２