Page 75 - 2025年第56卷第1期

表 ３ 不同方法计算值比较
流量 河宽 实测水深 床沙中径 计算水深 计算沙粒 沙波摩阻流速 水力 相对误差
方法 测站
３
∕（ｍ ∕ｓ） ∕ｍ ∕ｍ ∕ｍｍ ∕ｍ 水力半径∕ｍ ∕（ｍ∕ｓ） 参变数 ∕％
孙口 ９９５ ４７２ １．４２ ０．２４０ ３．１５ ０．５２ ０．０３ ５．１０ １．２２
孙口 ６４８ ３４４ １．４５ ０．３７１ ３．８９ ０．３２ ０．０２ １２．６３ １．６８
Ｅｉｎｓｔｅｉｎ 方法 孙口 ５４７ ３８１ １．１９ ０．２９２ ３．１５ ０．２８ ０．０２ １１．３５ １．６５
利津 ６３７ ３３７ １．７３ ０．２６２ ４．３５ ０．３６ ０．０２ １１．８４ １．５１
利津 ８０９ ２６７ ２．０６ ０．２０１ ４．２０ ０．７９ ０．０３ ４．０８ １．０４
孙口 ９９５ ４７２ １．４２ ０．２４０ ３．７３ ０．３９ ０．０２ ６．７３ １．６３
孙口 ６４８ ３４４ １．４５ ０．３７１ ４．５４ ０．２５ ０．０２ １６．２６ ２．１３
钱宁方法 孙口 ５４７ ３８１ １．１９ ０．２９２ ３．７１ ０．２２ ０．０２ １４．７３ ２．１１
利津 ６３７ ３３７ １．７３ ０．２６２ ４．７９ ０．３１ ０．０２ １３．８１ １．７７
利津 ８０９ ２６７ ２．０６ ０．２０１ ４．４１ ０．７３ ０．０３ ４．４２ １．１４
孙口 ９９５ ４７２ １．４２ ０．２４０ １．９６ ２．３２ ０．０５ １．１４ ０．３８
孙口 ６４８ ３４４ １．４５ ０．３７１ ２．２６ ２．２３ ０．０５ １．８４ ０．５６
简化后的
孙口 ５４７ ３８１ １．１９ ０．２９２ １．７９ １．９８ ０．０５ １．６３ ０．５１
本文方法
利津 ６３７ ３３７ １．７３ ０．２６２ ２．１６ ３．２６ ０．０５ １．２９ ０．２５
利津 ８０９ ２６７ ２．０６ ０．２０１ ２．４３ ３．９７ ０．０６ ０．８２ ０．１８

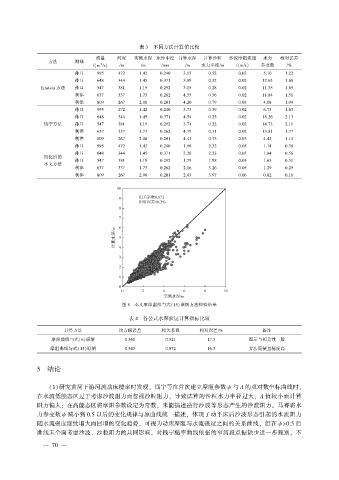
图 ８ 本文摩阻曲线与式（１５）联解方法检验结果

表 ４ 各公式水深验证计算指标比较

计算方法 均方根误差 相关系数 相对误差∕％ 备注
摩阻曲线与式（６）联解 ０．５６０ ０．８２１ １７．５ 图示与相关性一般
摩阻曲线与式（１５）联解 ０．５４３ ０．８７２ １６．３ 方法简便且精度高

５ 结论

（１）研究黄河下游河流动床糙率时发现， 钱宁等在首次建立摩阻参数 ψ 与 Ａ 的双对数坐标曲线时，
在水流低能态区过于考虑沙波阻力而忽视沙粒阻力， 导致试算的沙粒水力半径过大， Ａ 值较小而计算
阻力偏大； 在高能态区将摩阻参数设定为常数， 未能描述逆行沙波等形态产生的沙波阻力。 马睿将水
力参变数 ψ 减小到 ０．５ 以后的变化规律与原曲线统一描述， 体现了动平床后沙波形态引起的水流阻力
随水流强度继续增大而回增的变化趋势， 可视为动床摩阻与水流强度之间的关系曲线， 但在 ψ＞０．５ 后
曲线未全面考虑沙波、 沙粒阻力的共同影响， 对钱宁糙率曲线依据的窄河段点据缺少进一步甄别， 不

— ７ ０ —