Page 73 - 2025年第56卷第1期

（３）代入式（４）求得水力参变数 ψ；
（４）根据式（１２）计算出对应的 Ａ 值；
（５）将上述计算得到的数值代入式（９） 求
解出水深 ｈ′， 如此时的 ｈ′与假定的 ｈ 值不在误
差范围内， 则重新假定水深 ｈ 重复试算， 直至
二者相等。

４ 摩阻计算方法检验结果与方法改善

４．１ 检验数据来源 本研究中， 黄河下游选
取花园口、 夹河滩、 高村、 孙口、 艾山、 泺
口、 利津这 ７ 个水文站以及土城子段（泺口站
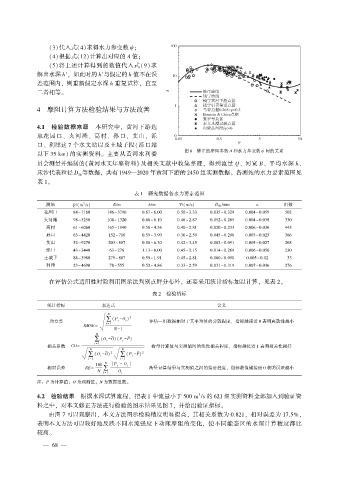
图 ６ 修正的摩阻参数 Ａ 和水力参变数 ψ 间的关系
以下 ３５ ｋｍ） 的实测资料。 主要从黄河水利委

员会测量并编制的《黄河水文年鉴资料》 及相关文献中收集整理， 得到流量 Ｑ、 河宽 Ｂ、 平均水深 ｈ、
床沙代表粒径 Ｄ 等数据， 共有 １９４９—２０２０ 年黄河下游的 ２４５０ 组实测数据。 各测站的水力要素范围见
５０
表 １。
表 １ 研究数据各水力要素范围
测站 Ｑ∕（ｍ ∕ｓ） Ｂ∕ｍ ｈ∕ｍ Ｖ∕（ｍ∕ｓ） Ｄ ５０ ∕ｍｍ ｎ 组数
３
花园口 ８４～７１６０ １４６～３７９０ ０．６７～６．００ ０．５０～３．３３ ０．０３５～０．３２９ ０．００４～０．０５９ ５０２
夹河滩 ９８～５２５０ １０８～１３２０ ０．６８～６．１０ ０．４６～２．８７ ０．０５２～０．２６５ ０．００４～０．０３８ ３３０
高村 ６１～６０６０ １６５～１９４０ ０．５８～４．３６ ０．４０～２．８１ ０．０２０～０．２３３ ０．００６～０．０３６ ４４５
孙口 ６３～４４２０ １５２～７１６ ０．５９～３．９０ ０．３６～２．５９ ０．０４５～０．２００ ０．００３～０．０２５ ３６６
艾山 ５２～９２７０ ２０３～８０７ ０．５６～６．３０ ０．４２～３．４５ ０．０６２～０．０９１ ０．００５～０．０２７ ２６８
泺口 ４３～３４４０ ６３～２７６ １．１３～８．００ ０．４５～２．１５ ０．０１４～０．２６９ ０．００６～０．０５６ ２３０
土城子 ８８～３９８０ ２７９～８０７ ０．５９～１．９１ ０．４５～２．８１ ０．０６０～０．０９０ ０．００５～０．０２ ３３
利津 ２３～４６９０ ７８～５５５ ０．５２～４．８６ ０．３３～２．５９ ０．０３１～０．３１９ ０．００７～０．０３６ ２７６

在评估公式适用性时除利用图示法判别点群分布外， 还要采用统计指标加以计算， 见表 ２。
表 ２ 检验指标
统计指标 表达式 含义
Ｎ
－
均方差 ∑ （Ｐ ｉ Ｏ ｉ ） ２ 评估一组数据相对于其平均值的分散程度， 指标越接近 ０ 表明离散性越小
ｉ ＝ １
ＲＭＳＥ ＝
Ｎ －１
Ｎ
－
－
∑ （Ｏ ｉ Ｏ）（Ｐ ｉ Ｐ）
ｉ ＝ １
相关系数 ＣＤ ＝ 衡量计算值与实测值间的线性相关程度， 指标越接近 １ 表明相关性越好
Ｎ Ｎ
－ ２
－ ２
∑ （Ｏ ｉ Ｏ） ∑ （Ｐ ｉ Ｐ）
ｉ ＝ １ ｉ ＝ １
Ｎ
１００ Ｐ ｉ － Ｏ ｉ
相对误差 ＲＥ ＝ ∑ 衡量计算结果与实测值之间的接近程度， 指标数值越接近 ０ 表明误差越小
Ｎ ｉ ＝ １ Ｏ ｉ
注： Ｐ 为计算值； Ｏ 为观测值； Ｎ 为数据组数。
４．２ 检验结果 根据水深试算流程， 把表 １ 中流量小于 ５００ ｍ ∕ｓ 的 ６２１ 组实测资料全部加入到验证资
３
料之中， 对本文修正方法进行检验的图示结果见图 ７， 并给出验证指标。
由图 ７ 可以观察出， 本文方法图示检验精度明显提高， 其相关系数为 ０．８２１， 相对误差为 １７．５％，
表明本文方法可以较好地反映不同水流强度下动床摩阻的变化， 使不同能态区的水深计算精度都比
较高。
— ６ ８ —