Page 71 - 2025年第56卷第1期

æ ρ －ρ Ｄ ö
３５
ｓ
力参变数 ψ 存在函数关系， 即 Ａ ＝ ｆç ÷ ， 并通过黄河下游花园口、 高村、 艾山、 土城子、 利津、
è ρ Ｒ′Ｊ ø
ｂ
前左 ６ 个水文站的实测资料点绘了 Ａ 与 ψ 间的关系图（图 ２）。
根据图 ２ 中点群分布， 钱宁等 ［２６］ 建立了黄河下游动床糙率关系曲线， 将糙率近似用下式表示：
２∕３
１∕６
Ｄ ψ ∕１２， ψ＞０．５
６５
ｎ ＝ １∕６ { （１０）
Ｄ ∕１９， ψ≤０．５
６５
钱宁等 ［２６］ 学者在给出 ψ－Ａ 曲线图时， 纵坐标采用的是只能反映泥沙粒径的摩阻参数 Ａ， 然而黄河
下游河床形态变化十分复杂， 水流强度的影响因素众多， 仅以 Ａ 反映河床糙率特性变化会导致使用图
中曲线得到的糙率计算结果与实测相差甚远 ［２７］ 。 同时， 横坐标 ψ 最大和最小时（分别代表水流强度最
小和最大的状态）， 图 ２ 中摩阻参数 Ａ 较小（对应的糙率大）的实测点据代表性并不好， 与黄河下游河
槽的条件差距较大。 具体讲， 当高能态区水流强度很大时， 绘制曲线采用了窄河段艾山、 利津水文站
流量 Ｑ＞７０００ ｍ ∕ｓ 的大流量资料， 在此条件下出现糙率较大值主要是窄河段两岸人工丁坝或山体边界
３
阻水严重影响造成的（利津测验断面两岸布设的大量丁坝呈现出犬牙交错的现象， 艾山测验断面属于
一岸有坝垛工程， 另一岸高水位时受山体边界影响很大）； 低能态区水流强度很小时采用了窄河段利
津水文站 Ｑ≤７０００ ｍ ∕ｓ 的点据与前左水文站的测验资料。 此外， 式（１０）中给出的 ψ≤０．５ 部分表达式
３
为指数型形式， 这样的表达式在图中近似显现为直线， 意味着水流强度大到一定程度后糙率不变， 而
Ｓｉｍｏｎｓ 等 ［２８］ 通过水槽实验探究了不同水流强度下的床面形态变化与河床阻力的关系， 发现随着水流
强度由弱变强， 河床阻力会经历增加段、 跌落段及再增加三个阶段， 即当糙率系数 ｎ 达到最小值后，
若水流强度进一步增大， 其会再缓慢增长。 由此可见， 图 ２ 曲线形式及其表达式（１０）在反映动床糙率关
系的问题上是不完善的。
利用黄河下游 ２４５０ 组实测数据中流量大于 ５００ ｍ ∕ｓ 的 １８２９ 组实测资料， 对式（１０） 进行计算检
３
３
验， 图 ３ 结果表明计算水深与实测水深的相对误差较大（如果包括 ６２１ 组流量小于 ５００ ｍ ∕ｓ 的资料，
点群分布则更加散乱）， 说明式（１０）不能用于实际工程中的糙率计算。

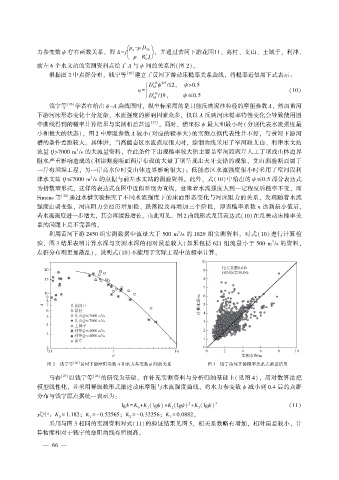
图 ２ 钱宁等 ［２６］ 黄河下游摩阻参数 Ａ 和水力参变数 ψ 间的关系 图 ３ 钱宁黄河下游糙率关系式验证结果

马睿 ［２７］ 以钱宁等 ［２６］ 的研究为基础， 在补充实测资料与分析归纳基础上（见图 ４）， 用对数算法把
模型线性化， 并采用幂级数形式描述动床摩阻与水流强度曲线， 将水力参变数 ψ 减小到 ０．４ 后的点群
分布与钱宁原点据统一表示为：
２ ３
ｌｇＡ ＝ Ｋ ＋Ｋ （ｌｇψ）＋Ｋ （ｌｇψ） ＋Ｋ （ｌｇψ） （１１）
０ １ ２ ３
式中： Ｋ ＝ １．１８２； Ｋ ＝ －０．５２５６５； Ｋ ＝ －０．３２２５６； Ｋ ＝ ０．０８８２。
０ １ ２ ３
采用与图 ３ 相同的实测资料对式（１１）的验证结果见图 ５， 相关系数略有增加， 相对误差较小， 计
算精度相对于钱宁的摩阻曲线有所提高。

— ６ ６ —