Page 70 - 2025年第56卷第1期

ρ －ρ Ｄ
ψ ＝ ｓ ３５ （４）
ρ Ｒ′Ｊ
ｂ
式中： ρ 、 ρ 为泥沙和水流的密度； Ｄ 为小于该粒径的重量占 ３５％的床沙粒径； Ｒ′为沙粒水力半径，
ｓ ３５ ｂ
这里实际引入了水力半径分割假定， 即取水力半径为沙粒阻力对应水力半径 Ｒ′和沙波阻力对应水力半
ｂ
径 Ｒ″之和：
ｂ
Ｒ ＝ Ｒ′＋Ｒ″ （５）
ｂ ｂ
式中 Ｒ′可由如下平均流速对数公式试算求得：
ｂ
æ χ Ｒ′ ö
ｂ
ｕ ＝ ５．７５ ｇＲ′Ｊ ｌｇ １２．２７ ÷ （６）
ç
ｂ
è ｋ ø
ｓ
式中： ｕ 为垂线上的平均流速； ｋ 为边界粗糙突起的高度， 可取 ｋ ＝ Ｄ ； ｇ 为重力加速度； χ 为修正系
ｓ ｓ ６５
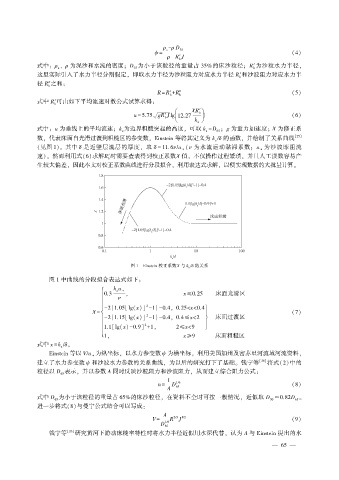
数， 代表床面自光滑过渡到粗糙区的参变数， Ｅｉｎｓｔｅｉｎ 等将其定义为 ｋ ∕δ 的函数， 并绘制了关系曲线 ［２５］
ｓ
（见图 １）。 其中 δ 是近壁层流层的厚度， 取 δ ＝ １１．６ν∕ｕ （ν 为水流运动黏滞系数； ｕ 为沙波摩阻流
∗ ∗
χ
速）。 然而利用式（６）求解Ｒ′时需要查表得到校正系数 值， 不仅操作过程繁琐， 并且人工读数容易产
ｂ
生较大偏差， 因此本文对校正系数曲线进行分段拟合， 利用表达式求解， 以便实现数据的大批量计算。

图 １ Ｅｉｎｓｔｅｉｎ 校正系数 χ 与 ｋ ｓ ∕δ 的关系

图 １ 中曲线的分段拟合表达式如下：
ｋ ｕ
ｓ ∗
０．３ ， ｘ≤０．２５ 床面光滑区
ν
２
－２｛１．０５［ｌｇ（ｘ）］ －１｝－０．４， ０．２５＜ｘ＜０．４ü
χ ＝ ï （７）
ï
－２｛１．１５［ｌｇ（ｘ）］ －１｝－０．４， ０．４≤ｘ＜２ ý 床面过渡区
２
ï
ï
２
１．１［ｌｇ（ｘ）－０．９］ ＋１， ２≤ｘ＜９ þ
１， ｘ≥９ 床面粗糙区
式中 ｘ ＝ ｋ ∕δ。
ｓ
Ｅｉｎｓｔｅｉｎ 等以 Ｖ∕ｕ 为纵坐标， 以水力参变数 ψ 为横坐标， 利用美国加州及密苏里河流域河流资料，
∗
建立了水力参变数 ψ 和沙波水力参数的关系曲线， 为以后的研究打下了基础。 钱宁等 ［２６］ 将式（２）中的
粒径以 Ｄ 表示， 并以参数 Ａ 同时反映沙粒阻力和沙波阻力， 从而建立综合阻力公式：
６５
１
ｎ ＝ Ｄ １∕６ （８）
Ａ ６５
式中 Ｄ 为小于该粒径的重量占 ６５％的床沙粒径， 在资料不全时可按一般情况， 近似取 Ｄ ≈０．８２Ｄ 。
６５ ５０ ６５
进一步将式（８）与曼宁公式结合可以写成：
Ａ
２∕３ １∕２
Ｖ ＝ Ｒ Ｊ （９）
Ｄ １∕６
６５
钱宁等 ［２６］ 研究黄河下游动床糙率特性时将水力半径近似用水深代替， 认为 Ａ 与 Ｅｉｎｓｔｅｉｎ 提出的水
— ６ ５ —