Page 74 - 2025年第56卷第1期

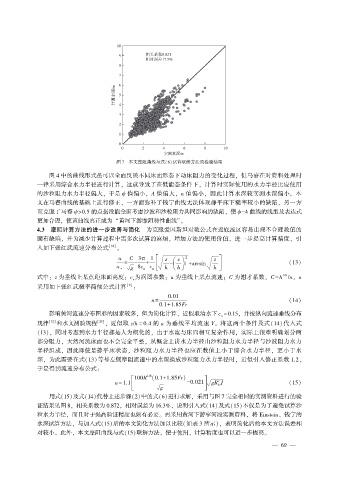
图 ７ 本文摩阻曲线与式（６）试算联解方法的检验结果

图 ４ 中的曲线形式虽可以全面反映不同床面形态下动床阻力的变化过程， 但马睿在对资料处理时
一律采用综合水力半径进行计算， 这就导致了在低能态条件下， 计算时实际使用的水力半径比应使用
的沙粒阻力水力半径偏大， 于是 ψ 值偏小， Ａ 值偏大， ｎ 值偏小， 因此计算水深较实测水深偏小。 本
文在马睿曲线的基础上进行修正， 一方面弥补了钱宁曲线无法体现静平床下糙率较小的缺陷， 另一方
面克服了马睿 ψ＞０．５ 的点据没能全面考虑沙波和沙粒阻力共同影响的缺陷， 使 ψ－Ａ 曲线的线型及表达式
更加合理， 使该曲线真正成为 “黄河下游摩阻特性曲线”。
４．３ 摩阻计算方法的进一步改善与简化 为克服爱因斯坦对数公式在近底流区容易出现不合理数值的
固有缺陷， 并为减少计算过程中需多次试算的麻烦， 增加方法的使用价值， 进一步提高计算精度， 引
入如下张红武流速分布公式 ［３２］ 。
ｕ Ｃ ３π １ é ｚ æ ｚ ö ２ ｚ ù
＝ － ＋ ê －ç ÷ ＋ａｒｃｓｉｎ ú （１３）
ｕ ｇ ８ｃ ｃ ê ｈ è ｈ ø ｈ û ú
∗ ｎ ｎ ë
式中： ｚ 为垂线上某点距床面高度； ｃ 为涡团参数； ｕ 为垂线上某点流速； Ｃ 为谢才系数， Ｃ ＝ ｈ ∕ｎ， ｎ
１∕６
ｎ
采用如下张红武糙率简便公式计算 ［９］ ：
０．０１
ｎ ＝ （１４）
０．１＋１．８５Ｆｒ
影响黄河流速分布图形的因素较多， 但为简化计算， 近似取清水下 ｃ ＝ ０．１５， 并按纵向流速垂线分布
ｎ
规律 ［３２］ 和水文测验规程 ［２９］ ， 近似取 ｚ∕ｈ ＝ ０．４ 的 ｕ 为垂线平均流速 Ｖ。 将这两个条件及式（１４） 代入式
（１３）， 同时考虑到水力半径都是人为概化的， 由于水流与床面相互复杂作用， 实际上很难明确划分两
部分阻力， 天然河流床面也不会完全平整， 从概念上讲水力半径由沙粒阻力水力半径与沙波阻力水力
半径组成， 因此即使是静平床状态， 沙粒阻力水力半径也应在数值上小于综合水力半径， 更小于水
深， 为此需要在式（１３）等号左侧摩阻流速中的水深换成沙粒阻力水力半径时， 近似引入修正系数 １．２，
于是得到流速分布公式：
１∕６
é １００Ｒ （０．１＋１．８５Ｆｒ） ù
ｕ ＝ １．１ ê －０．０２１ú ｇＲ′Ｊ （１５）
ê ú ｂ
ë ｇ û
用式（１５）及式（１４）代替上述步骤（２）中的式（６）进行求解， 采用与图 ７ 完全相同的实测资料进行的验
证结果见图 ８， 相关系数为 ０．８７２， 相对误差为 １６．３％， 说明引入式（１４）及式（１５）不仅是为了避免试算沙
粒水力半径， 而且对于提高验证精度也颇有必要。 再采用黄河下游窄河段实测资料， 将 Ｅｉｎｓｔｅｉｎ、 钱宁的
水深试算方法， 与加入式（１５）后的本文简化方法加以比较（如表 ３ 所示）， 表明简化后的本文方法误差相
对较小。 此外， 本文摩阻曲线与式（１５）联解方法， 便于使用， 计算精度也可以进一步提高。

— ６ ９ —