Page 72 - 2025年第56卷第1期
P. 72
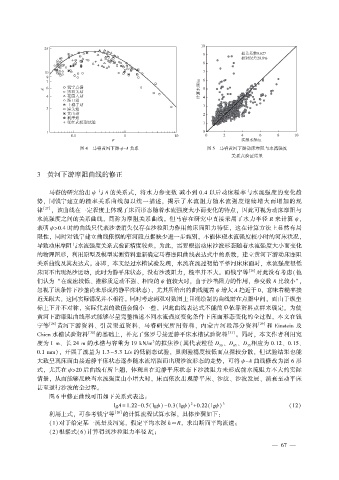
图 4 马睿黄河下游 ψ-A 关系 图 5 马睿黄河下游动床摩阻与水流强度
关系式验证结果
3 黄河下游摩阻曲线的修正
马睿的研究给出 ψ 与 A 的关系式, 将水力参变数 减小到 0.4 以后动床糙率与水流强度的变化趋
势, 同钱宁建立的糙率关系曲线加以统一描述, 揭示了水流阻力随水流强度继续增大而增加的规
律 [27] , 该曲线在一定程度上体现了床面形态随着水流强度大小而变化的特点, 因此可视为动床摩阻与
水流强度之间的关系曲线, 简称为摩阻关系曲线。 但马睿在研究中直接采用了水力半径 R 来计算 ψ,
表明 ψ>0.4 时的曲线只代表沙垄消失仅存在沙粒阻力作用的床面阻力特征, 这在计算方法上显然有局
限性, 同时对钱宁建立曲线依据的窄河段点据缺少进一步甄别, 不能体现水流强度较小时的河床状况,
导致动床摩阻与水流强度关系式验证精度较差。 为此, 需要根据动床沙波形态随着水流强度大小而变化
的物理图形, 利用原型及模型实测资料重新确定马睿摩阻曲线表达式中的系数, 建立黄河下游动床摩阻
关系曲线及其表达式。 亦即, 本文经过水槽试验发现, 水流在流过初始平整河床床面时, 水流强度很低
床面不出现泥沙运动, 此时为静平床状态, 没有沙波阻力, 糙率并不大。 而钱宁等 [26] 对此没有考虑(他
们认为 “在流速较低、 推移质运动不强、 相应的 ψ 值较大时, 由于沙垄阻力的作用, 参变数 A 比较小”,
忽视了该条件下沙垄尚未形成的静平床状态), 尤其所给出的曲线随着 ψ 增大 A 趋近于 0, 意味着糙率接
近无限大, 这同实际情况并不相符。 同时考虑到双对数图上目视绘制的曲线需在点群中间, 而由于纵坐
标上下并不对称, 实际代表的数值会偏小一些, 因此曲线表达式不能简单依靠资料点群来确定。 为使
黄河下游摩阻曲线形式能够尽量完整描述不同水流强度变化条件下床面形态变化的全过程, 本文在钱
宁等 [26] 黄河下游资料、 引黄渠道资料、 马睿研究所用资料、 内蒙古河段部分资料 [29] 和 Einstein 及
Chien 水槽试验资料 [30] 的基础上, 补充了张罗号接近静平床水槽试验资料 [31] 。 同时, 本文作者利用宽
3
度为 1 m、 长 24 m 的水槽与容重为 19 kN∕m 的拟焦沙(其代表粒径 D 、 D 、 D 相应为 0.12、 0.15、
50 65 35
0.1 mm), 开展了流量为 1.3~5.3 L∕s 的低能态试验, 虽测验精度较低而点据较分散, 但试验结果也能
大致呈现床面由接近静平床状态逐步随水流增强而出现沙波形态的走势, 可将 ψ-A 曲线修改为图 6 形
式, 尤其在 ψ>20 后曲线有所上翘, 体现出在近静平床状态下沙波阻力未形成前水流阻力不大的实际
情景, 从而能够反映当水流强度由小增大时, 床面依次出现静平床、 沙纹、 沙波发展、 消衰至动平床
甚至逆行沙波的全过程。
图 6 中修正曲线可用如下关系式表达:
2
lgA = 1.22-0.5(lgψ)-0.3(lgψ) +0.22(lgψ) 3 (12)
利用上式, 可参考钱宁等 [26] 的计算流程试算水深, 具体步骤如下:
(1)对于给定某一流量及河宽, 假定平均水深 h≈R, 求出断面平均流速;
(2)根据式(6)计算得到沙粒阻力半径 R′;
b
— 6 7 —