Page 50 - 水利学报2025年第56卷第4期
P. 50
刻最终的输出信息,具体公式如下:
f t = σ (W f[ h t - 1 ,x t] + b f ) (1)
i t = σ (W i[ h t - 1 ,x t] + b i ) (2)
C′ t = tanh(W c[ h t - 1 ,x t] + b c ) (3)
(4)
C t = f t ⊗ C t - 1 + i t ⊗ C′ t
O t = σ (W o[ h t - 1 ,x t] + b o ) (5)
(6)
h t = O t tanh ⊗ C t
P t = ( f (D t ,D t - 1 ,D t - 2 ,…,D t - 7 )) (7)
式中:x 为输入向量;h 为上一单元状态的输出信息;σ 为 sigmoid 函数;tanh 为激活函数;C 为当前
t
t
t-1
记忆单元信息;C 为上一单元记忆输出;C′ t 为整合之后的最新记忆信息;h 为本单元的输出信息;⊗表示向
t-1 t
量相乘;W 、W 、W 和 W 为神经网络的权重矩阵;b、b、b 和 b 为偏置向量 [24] ;(D t , D t - 1 , D t - 2 , …, D t - 7 )
c
f
i
c
i
o
f
o
为不同年份旱涝数据代表输入向量 x ;f()代表式(1)—(6)的整个过程;P 为输出信息降水。
t
t
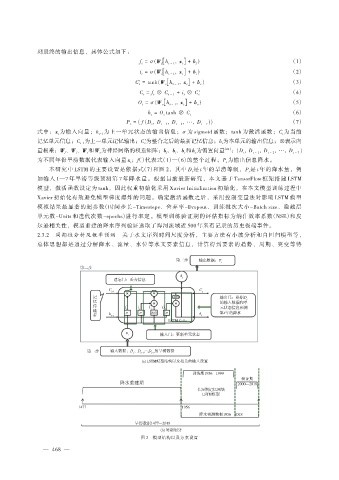
本研究中 LSTM 的主要设置是依据式(7)和图 2,其中 D 是 t 年的旱涝等级,P 是 t 年的降水量,例
t
t
如输入 1—7 年旱涝等级预测第 7 年降水量。根据目前最新研究,本文基于 TensorFlow 框架搭建 LSTM
模型,激活函数设定为 tanh,因此权重初始化采用 Xavier Initialization 初始化,在本文模型训练过程中
Xavier 初始化有效避免模型梯度爆炸的问题。确定激活函数之后,采用控制变量法对影响 LSTM 模型
模拟结果最显著的超参数(时间步长-Timesteps、舍弃率-Dropout、训练批次大小-Batch size、隐藏层
单元数-Units 和迭代次数-epochs)进行率定。模型训练验证期的评估指标为纳什效率系数(NSE)和皮
尔逊相关性,模型重建的降水序列验证选取了海河流域近 500 年来有记录的历史极端事件。
2.3.2 周期性分析及概率预测 关于水文序列时间尺度分析,主要方法有小波分析和自回归模型等,
总体思想都是通过分解降水、流量、水位等水文要素信息,计算得到要素的趋势、周期、突变等特
图 2 模型结构以及方案设置
— 468 —