Page 63 - 2021年第52卷第10期

d
调蓄水量，m ； q 为 t 时段 d 日入库流量，m /s；Δd 为一天的秒数。
3
3
t
由于蓄水期来水较多，可认为最小下泄流量需求总可以满足，则式（1）总能成立，因此图 1 中横
d
坐标可转换为 A = q Δd ，即可用水量等于天然来水量。假定月内最大发电流量不变，在水库不蓄水
t
情况下（ k = 0），根据图 1 中风险最小蓄水规则（ABDE）能够得到 t 时段不蓄弃水量为：
D t
t å
d
W = w ，t ∈ Ω （3）
t
d = 1
其中：
d
ì0 q ≤ Q t max
t
ï
d
w = í d max d max （4）
t
ï q - Q
î ( t t ) Δd q > Q t
t
d
式中： Q t max 为 t 时段最大发电流量限制，m /s； w 为 t 时段 d 日不产生弃水所需拦蓄的水量，m 。
3
3
t
以月为尺度计算不蓄水情况下时段 t 的最小弃水量为：
ì0 q ≤ Q t max
t
ï
W ′ = í max max （5）
t
ï q - Q
î ( t t ) D Δd q > Q t
t
t
D t
d
式中： q 为 t 时段水库平均入库流量， q = D å q ，m /s。
1
3
t
t
t
t d = 1
W 代表考虑月内径流波动后不蓄水情况下的最小弃水量估计，其与 W ′ 间的关系有三种情况：
t t
d
d
情 况 1。 ∀d 满 足 q ≤ Q t max ， 则 W = W ′ = 0 ； 情 况 2。 ∀d 满 足 q > Q t max ， 根 据 式（5）得 到
t
t
t
t
d
d
W = W ′ = ( q - Q t max ) D Δd ；情况 3。∃d 使 q ≤ Q t max ，且∃d 使 q > Q t max ，根据式（4）和（5）可得
t
t
t
t
t
t
出 W > W ′ 。
t t
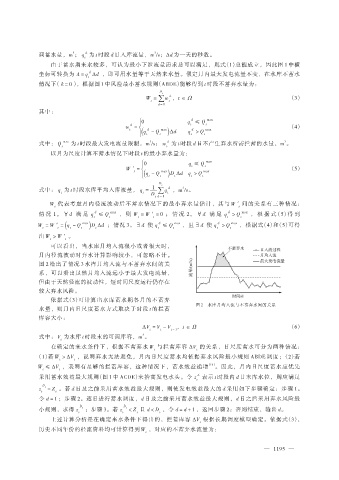
可以看出，当水库月均入流很小或者很大时，
月内径流波动对弃水计算影响较小，可忽略不计。
图 2 给出了情况 3 水库月均入流与不蓄弃水间的关
系，可以看出虽然月均入流远小于最大发电流量，
但由于天然径流的波动性，短时间尺度运行仍存在
较大弃水风险。
依据式（3）可计算出水库蓄水期各月的不蓄弃
图 2 水库月均入流与不蓄弃水间的关系
水量，则月内日尺度蓄水方式取决于时段 t 的拦蓄
库容大小：
ΔV = V - V ，t ∈ Ω （6）
t t t - 1
式中： V 为水库 t 时段末的可调库容，m 。
3
t
在确定的来水条件下，根据不蓄弃水 W 与拦蓄库容 ΔV 的关系，日尺度蓄水可分为两种情况：
t
t
（1）若 W > ΔV ，说明弃水无法避免，月内日尺度蓄水均依据弃水风险最小规则 ABDE 调度；（2）若
t
t
W ≤ ΔV ，表明有足够的拦蓄库容，这种情况下，蓄水效益递增 ［16］ 。因此，月内日尺度蓄水应优先
t
t
采用蓄水效益最大规则（图 1 中 ACDE）来抬高发电水头。令 z t d 表示 t 时段内 d 日末库水位，则应满足
z t D t = Z 。若 d 日及之前采用蓄水效益最大规则，则使发电效益最大的 d 采用如下步骤确定：步骤 1。
t
令 d = 1 ；步骤 2。逐日进行蓄水调度，d 日及之前采用蓄水效益最大规则，d 日之后采用弃水风险最
D D
小规则，求得 z t t ；步骤 3。若 z t t < Z 且 d < D ，令 d = d + 1 ，返回步骤 2；否则结束，输出 d。
t
t
上述计算分析是在确定来水条件下得出的，拦蓄库容 ΔV 根据长期调度模型确定。依据式（3），
t
历史不同年份的径流资料均可计算得到 W ，对应的不蓄弃水流量为：
t
— 1195 —