Page 25 - 2023年第54卷第7期

模型得如图 ６所示的计算结果，图中：实线和虚线分别表示不考虑空气阀高度（ｈ ＝ ０．０ｍ）和考虑空
气阀高度。

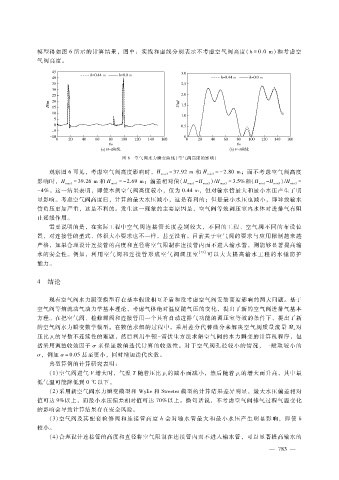
图 ６ 空气阀水力瞬变曲线（空气阀高度的影响）

观察图 ６可见，考虑空气阀高度影响时，Ｈ ＝ ３７．９２ｍ和 Ｈ ＝－ ２．８０ｍ；而不考虑空气阀高度
ｍａｘ３ ｍｉｎ３
影响时，Ｈ ｍａｘ１ ＝ ３９．２６ｍ和 Ｈ ｍｉｎ１ ＝－ ２．６９ｍ；偏差相对值（Ｈ ｍａｘ１ － Ｈ ｍａｘ３ ）?Ｈ ｍａｘ３ ＝ ３．５％和（Ｈ ｍｉｎ１ － Ｈ ｍｉｎ３ ）?Ｈ ｍｉｎ３ ＝
－ ４％。这一结果表明，即使本例空气阀高度较小，仅为 ０．４４ｍ，但对输水管最大和最小水压产生了明
显影响。考虑空气阀高度后，计算的最大水压减小，这是有利的；但是最小水压也减小，即导致输水
管负压更加严重，这是不利的。发生这一现象的主要原因是，空气阀等效调压室内水体对进排气有阻
止延缓作用。
需要说明的是，在实际工程中空气阀连接管长度差别较大，不同的工程、空气阀不同的布设位
置，对连接管的型式、体积大小要求也不一样，甚至没有。目前关于空气阀的要求与应用限制越来越
严格，如果合理设计连接管的高度和直径将空气限制在连接管内而不进入输水管，则能够显著提高输
水的安全性。例如，利用空气阀和 连接 管 形 成空气阀 调 压室 ［１３］ 可 以大 大提 高输 水工 程的 水 锤防护
能力。

４ 结论

现有空气阀水力瞬变模型存在基本假设相互矛盾和没考虑空气阀安装高度影响的两大问题。基于
空气阀等熵流动气动力学基本理论，考虑气体绝对温度随气压的变化，提出了新的空气阀进排气基本
方程。在把空气阀、检修蝶阀和连接管用一个具有自动进排气功能的调压室等效的条件下，提出了新

的空气阀水力瞬变数学模型。在数值求解的过程中，采用差分代替微分来解决空气阀质量流量 Ｍ 对
ａ
压比 ｐ的导数不连续性的难题，然后利用牛顿 － 雷伏生方法求解空气阀的水力瞬变的计算机程序，包
ｒ
括采用调整收敛因子 σ来保证数值迭代计算的收敛性。对于空气阀孔径较小的情况，一般取较小的
σ ，例如 σ ＝ ０．０５ 甚至更小，同时增加迭代次数。
典型算例的计算研究表明：
（ １）空气阀进气 Ｖ增大时，气温 Ｔ随着压比 ｐ的减小而减小，然后随着 ｐ的增大而升高，其中最
ｒ
ｒ
低气温可能降低到 ０℃以下。
（ ２）采用新空气阀水力瞬变模型和 Ｗｙｌｉｅ和 Ｓｔｒｅｅｔｅｒ模型的计算结果差异明显，最大水压偏差相对
值可达 ９％以上，而最小水压偏差相对值可达 ７０％以上。换句话说，不考虑空气阀排气过程气温变化
的影响会导致计算结果存在安全风险。
（ ３）空气阀及其配套检修阀和连接管高度 ｈ会对输水管最大和最小水压产生明显影 响，即使 ｈ
较小。
（４）合理设计连接管的高度和直径将空气限制在连接管内而不进入输水管，可以显著提高输水的

— ７ ８ ３ —